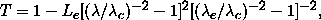
This survey is a very large project and brings technology and techniques which are quite new to astronomy. It is clear that if it is to be successful its planning will have to proceed very carefully, and the many tradeoffs between efficiency and cost on the one hand and the quality of the data on the other must be weighed cautiously. The strategy we are currently planning to follow is outlined in this chapter, along with the motivation for doing what we plan to do. It may still change slightly as we learn more, finish building the hardware, and dream of yet new scientific rewards to be reaped with only small changes in the way we do things.
The purpose of the photometric survey is fourfold: first, to identify and provide positions for a uniformly-selected sample of galaxies, of which the ~ 900,000 galaxies with r' < 18.15 Petrosian magnitudes and the ~ 100,000 luminous red galaxies will constitute the spectroscopic survey; second, to provide precise colors and approximate morphological information for that sample; third, to provide the database needed for identification of quasars by image structure and apparent color; fourth -- wouldn't you really like to have a reliable photometric catalog of the brightest 5 x 107 galaxies and a comparable number of stars, over some substantial region of sky, with 3% or better colors in five broad filters?
The major factors that need to be addressed in specifying parameters for the photometric survey are angular resolution (pixel size), field size, exposure time, and exposure strategy.
There are many factors which lead one to consider the time-delay-and- integrate (TDI) or `scanning' mode as the exposure strategy of choice.
First, it results in essentially 100 per cent observing efficiency, since the data are taken and recorded as the exposure progresses. Even with 4-quadrant readout available in the Tek/SITe 2048x2048 CCDs, it requires about 30 seconds to read a chip, and of the order of 7 seconds to prepare one for a new exposure. This has to be compared with the 55 second exposure time provisionally adopted for the survey; readout time would probably dominate the setting time to the next field, but one still has a 67% overhead compared with TDI. The only efficiency loss with TDI is the ramp-up and ramp-down time (one must start a full frame height before taking data and go a full frame height beyond the end of the imaging region for complete data retrieval; even if resuming a previously stopped scan, one must go a chip height). This makes TDI rather inefficient for pictures of a single object, but if one is to scan for hours, a few minutes at the beginning and end hardly matter.
Second, the fact that each object traverses each chip vertically reduces the flat-fielding problem to one dimension, and most column trap-type defects which do not completely block charge transfer disappear. Flat-fielding problems, especially severe in the near-IR because of the complexity of the sky spectrum, completely disappear even for badly-behaved devices. The flat fields can also be generated on the fly with median techniques looking directly at the background, since the background is dynamic and a given horizontal pixel is sky most of the time. These techniques have been developed for the four-shooter scanning surveys at Palomar by Schneider and Gunn (cf. Schneider et al. 1989) and work very well.
Finally, the technique facilitates multicolor photometry with good time response if the focal plane is big enough; our focal plane puts six columns of five chips each along the scan direction, with five different filters (see the discussions in Chapters 2 and 4) for our five bands u' , g' , r' , i' , and z' . The total elapsed time across the array is about 5.6 minutes.
The difficulties with TDI are not negligible, but are, we believe, surmountable. The optical design must have very low distortion; this is addressed in Chapter 2, and we have a design which is excellent from this viewpoint. Second, the chips must be exquisitely aligned rotationally, so that stars traverse columns very accurately. For a 2048 x 2048 chip, if we want no more than 0.25 pixel error (which is easy to measure) the rotational alignment must be better than 1 arcminute. This is not, in fact, difficult to do, but one must be careful. We will try to do at least factor of two better.
The issue of exposure time is, to some extent, a matter of taste. We will see that we get a quite good signal-to-noise ratio on galaxy images near the spectroscopic limit, and could, in principle, back off a little on our proposed integration time, but there are some technical limitations. If we scan at the sidereal rate, 15 arcseconds/second, (which is not accomplished by simply parking the telescope for any declination except 0°) the time taken by a star to cross the 13.5 arcminute field of one CCD is 55 seconds, and so that is the exposure time for that rate. At that rate, the line rate for each chip is 37.5 lines/second, and the pixel rate about 77 kHz. Tektronix/SITe kindly splits the serial register into two halves, so we need read only half the 2048 pixels (plus 20 extended register pixels and 20 overscan pixels), through each amplifier, for a rate of about 38 kHz. This is nearly optimal; the read noise rises like the square root of the rate when one goes much faster than this, and the read noise is already a major contributor to the noise at u' ; for a rate twice sidereal, the flux is down a factor of 2 (to about 19 per pixel in the sky) in u' , the nominal noise is up to 7 electrons, and the readout noise completely dominates. Since our u' sensitivity is none too good anyway, this quickly becomes catastrophic. There are other problems, such as suitably accurate and sufficiently inexpensive 16-bit A/D converters not being fast enough. So going significantly faster is problematic. At the sidereal rate, the imaging survey will take about 20-25% of the survey time, so going faster does not really save very much in any case. Going slower would have considerable impact upon the time-to-completion, not so much because of the time added but because we expect conditions to be good enough for the imaging survey (good seeing and photometric) not more than about a quarter of the time. Thus a rate near sidereal, and consequently an exposure time of about a minute, appears to be about optimal; we will assume the sidereal rate throughout this document.
For a given duration for the survey, we wish to maximize simultaneously the total number of galaxies, the survey depth, the linear scale projected on the sky, and the degree of completeness. The nominal survey objective is to obtain redshifts for 10 6 galaxies. The largest contiguous solid angle that can be surveyed from one hemisphere that excludes the Galactic plane is about pi steradians, corresponding to a cone with an opening angle of 120°. Within this area there are ~ 106 galaxies brighter than r' = 18.15 ; this limit is about 5 times deeper than the current B = 15.5 surveys, and there is good sensitivity to large-scale structure to z ~ 0.2.
The geometric boundaries of the survey region need to be considered in some detail. The cone b > 30° seems natural, but there are severe problems with it. The latitude of the site is 32.8°, which carries the southern boundary of the survey to an altitude of 24.6deg at transit ( delta = -32.6°). At that altitude differential refraction effects are catastrophic. If we apply the prescription of Burstein and Heiles (1978) for Galactic extinction to the Heiles (1975) HI maps with or without his `residual' galaxy count maps (Heiles 1976) we also see that a region centered on the pole is not the best if one is attempting to use the largest contiguous region of low extinction. In particular, the region near longitude 0° has much higher extinction than the one in the anticenter direction, and one should tip the region by several degrees in that direction. It hurts not at all from the extinction point of view to tip it northward in declination as well, nor to make it slightly elliptical so that its declination extent is not quite so great as the extent in right ascension. We have finally provisionally decided on an elliptical region centered at 12h 20m , +32.8° (so that it passes overhead), whose minor axis is the meridian at that right ascension, with extent +-55° in declination. The major axis is the great circle perpendicular to that, and the extent is +- 65°; it extends from about 7h 6m to about 17h 34m . The most southerly declination is -22°, so if one stays near the meridian when working in the South, the minimum altitude is about 35°, which is manageable. Tipping to earlier right ascension has another benefit which is probably fully as important as the absorption; the site suffers from the same monsoon season as Kitt Peak, and pushing the `prime time' a little earlier in the year is a boon, not to mention the fact that the nights are longer. The survey footprint as presently defined is compared with the extinction contours calculated from the HI column densities measured by Stark et al. (1992) in Figure 1.1. We have tentative plans to rotate the ellipse by ~ 20° to match regions of low extinction better, and will use the extinction contours derived from the COBE/DIRBE maps by Schlegel (1995). The detailed considerations are summarized by Kent (1996).
The footprints of the Northern and Southern SDSS surveys. The tracks for the photometric survey are shown by heavy lines. The contours show the extinction measured from the HI column density.
We should spend some time here considering the strategy "in the large" for the photometric survey; i.e. how we in fact scan to cover the survey region. We defined this above as an elliptical area on the sky, 110° by 130°. It is clear that we must scan along great circles in the sky to minimize transit-time differences across the imaging CCD array, which with the telescope/camera design presented in Chapters 2 and 4 is 2.5° square; the projection errors from the finite size of the array are only just negligible for our field, and we cannot deviate appreciably from the great circle requirement. It seems reasonable to scan as nearly as we can in right ascension, to minimize the motion of the telescope and the change in airmass in a given scan. This suggests that we arrange the scanning in the following manner: (see Figures 1.1, 1.2 and 1.3).
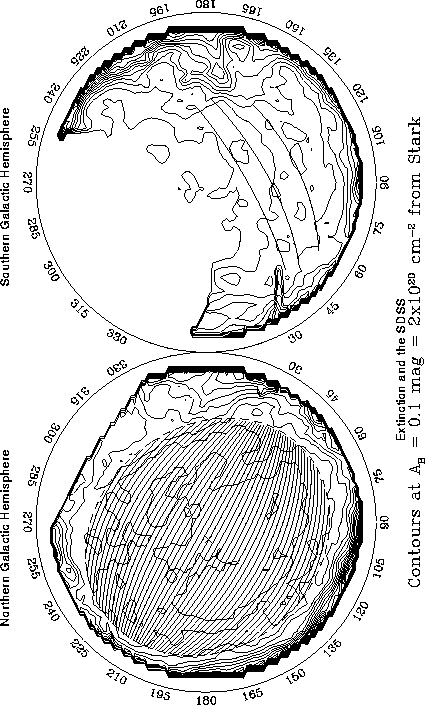
Projection on the sky of SDSS survey area. `N' is the North Celestial Pole. The stripe longitude lambda is measured from the survey central meridian positive to the east along the great circles perpendicular to that meridian; the latitude eta is measured along that meridian to the relevant great circle, positive to the north. The plot is centered on lambda , eta = 0,0. The positions of the stars in the Yale Catalogue of Bright Stars are shown down to about 7th magnitude. The largest symbols represent 0m stars and the smallest stars of 5m and fainter. The Monitor Telescope patches are shown as squares and are placed 6 per 15° of lambda to avoid bright stars.
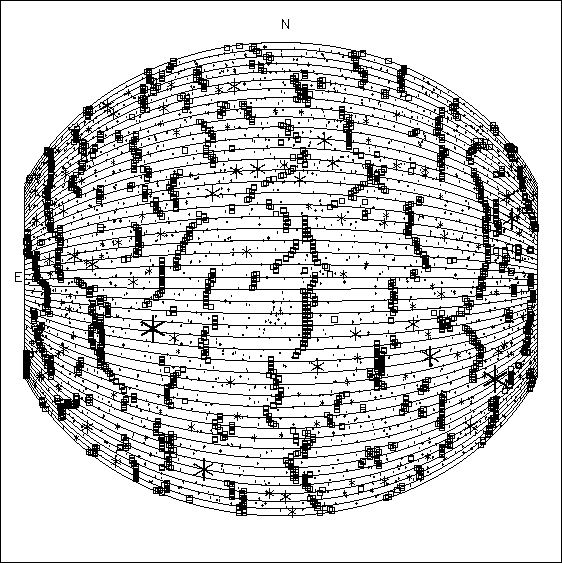
Right ascension-declination grid superposed on the survey area. The projection is the same as in Figure 1.2.
The meridian which passes through the center of the survey area, 12h 20m , defines the central meridian of the scan. The great circle perpendicular to it passing through the survey center at delta =32.8deg; is the survey equator. A point in the survey region is defined by a survey latitude eta which is the angle between the survey equator and the great circle passing through the point perpendicular to the survey meridian, and a survey longitude lambda measured positively eastward from the survey meridian to the point along that great circle. Note that the nature of the constant longitude and latitude curves is backwards from the usual; the constant latitude curves are great circles, and the constant longitude curves are circles centered on the survey poles, in this case an east pole and a west one, at delta = 0 , alpha = 18h 20m and 6h 20m . The constant latitude curves are the scan tracks. A single scan, called a strip, must be combined with another to make a filled stripe about 2.5 degrees wide. The constant latitude lines converge toward the survey poles, so the two strips in a stripe cannot be centered on great circles. Instead, a suitable track in the array, about a half-chip width away from the center (cf. Figure 2.2) tracks the great circle which is the stripe equator; the other strip then uses the other one.
The strips need not be scanned their full length at one time; if one does, they are 8h 40m long at the survey equator, decreasing only very slowly as one goes to higher or lower survey latitude. There are 45 stripes, 90 strips, in the survey; this is one more than the arithmetic would suggest, but having a fiducial stripe centered on declination 0°, where one can just park the telescope, will be very valuable indeed. There is clearly a lot of overlap in the stripes as one approaches the survey poles; this amounts to about 28% over the area of the survey (expressed as the fraction of the area of sky covered twice). At the ends of the stripes closest to the poles there is, in fact, a small region near the center of each stripe which is covered by three stripes. The southernmost and northernmost stripes dip to 35° altitude on the survey meridian and should be done very close to the meridian under the very best conditions; otherwise, it seems prudent for the sake of keeping the data most useful as one progresses to build contiguously out from the survey equator. It may have an unfortunate effect on the spectroscopic tiling strategy (Chapter 8) to have three such growing regions, but it is probably necessary for the sake of the homogeneity of the survey.
The specific tradeoff of pixel size versus field size is addressed by fixing the pixel size first and then stuffing the focal plane with enough CCDs to use the entire field, which should have been designed as large as possible. Actually, it does little good to pack the CCDs across the scan direction much closer than their sizes, since one must always make two passes to cover the sky. The tradeoff here is how much sky one wishes to cover twice, since sampling twice gives one all manner of useful data. We have here, largely for mechanical and economic reasons, chosen to have a quite small overlap from one scan to the next, only about 8%.
For identifying galaxies and studying galaxy morphology, it is essential that the pixel size be small enough to take advantage of the best seeing. Morphological typing of galaxies is important in a number of applications, and we consider the morphological and color data which will emerge from this survey an absolutely necessary part of the survey, without which the redshift data are far less valuable.
The required pixel size is proportional to the size of the seeing disk (by which we mean here the total image size, as contributed to by seeing, optics, tracking, etc. -- but clearly one wants it to be dominated by seeing), and typical seeing varies considerably with site, and with telescope at a given site. At the 4-m Mayall telescope the median full width at half-maximum is about 1 arcsecond, and at the Multiple Mirror Telescope the median is about 0.8 arcsecond. One should sample the seeing disk with no fewer than 2 pixels per full width at half-maximum, and a scale of 0.4 arcsecond per pixel then provides proper sampling for seeing that is characteristic of the Multiple Mirror Telescope site, and, we believe, for Apache Point. Our error budget is such that we will attain 1-arcsecond images when the seeing is 0.8 arcseconds, and our sampling will be more than adequate unless the seeing is very good.
The classification of images as either stars or galaxies depends on the pixel scale, the seeing, and the signal-to-noise ratio per pixel. For this purpose one wants to use the largest pixels possible while still being able to recognize the most compact galaxies at the survey limit. As a secondary consideration, the pixels should be small enough that star contamination does not seriously impair galaxy identification or photometry. Given arbitrarily high signal-to-noise ratio and perfect flat-fielding, even poorly resolved galaxies can be distinguished from stars, so one must find the best compromise between pixel scale and integration time. The dominant source of noise is statistical fluctuations in the night sky. The dominant source of systematic error in the night sky is a combination of bad flat-fielding, interference from nearby objects, and scattered light from bright stars. In crowded fields (e.g., in a cluster of galaxies or at low Galactic latitude) the latter two are serious; with CCDs of the quality obtainable today and especially in TDI mode, flat-fielding errors are completely negligible. It would appear that one could get by with somewhat bigger pixels for this problem than that of morphology, since differences between galaxy profiles (particularly small de Vaucouleurs ones) and stars are most sensitively detected at about 1 seeing diameter away from the center; having smaller pixels, however, is clearly all to the good so long as there is enough charge so that shot noise dominates the read noise.
The most difficult galaxies to identify are compact ellipticals (because they look like stars) and low surface brightness objects (not because they are difficult to classify, but because they are hard to find). Consider the former. Without moon, the night sky has a surface brightness µr = 20.8 (Thuan-Gunn (1976) r system). Galaxy profiles can be measured to a surface brightness µr = 24 mag arcsecond-2 reliably but systematic errors start to dominate at fainter levels. Photometry of bright field galaxies shows that most have a mean surface brightness within the µr = 24 mag arcsecond-2 isophote in the range µ24= 21.5 to 22.5 , nearly independent of morphological type (Kent 1985). At a minimum, the survey must identify objects at µ24= 21.5 reliably (compact ellipticals like M32 have µ24<= 21.0 ).
We have done fairly extensive simulations of the survey imaging data (cf. Chapter 9) to investigate questions like these; For example, a compact elliptical with an effective radius of about 1.5 pixels (0.6 arcsecond) at z=0.216 , at which redshift it is slightly beyond the spectroscopic survey limit ( r'=18.15 ). Tests with the MIRAGE object finder and classifier reject this object's being a star at the 20 sigma level, and a magnitude fainter and 20% smaller, at z=0.288 , still at 10 sigma . At a redshift of 0.576 in the red, at which point the effective radius is 0.35 arcsecond and the total S/N a factor of three smaller than the case at the survey limit in r' , it is still 4.5 sigma away from a star. Indeed, at the survey limit the difference between a de Vaucouleurs law classification and an exponential is 3.2 sigma , so simple classifiers can do very well at this brightness level, which is not at all surprising when one looks at the images in the simulations. Indeed the software which reduces the imaging data works this well (Chapter 10).
At the other extreme, that of low surface brightness galaxies, we should be able to do very well indeed; objects of the size of the very low surface brightness galaxy Malin 1 (see Impey and Bothun 1989) will be detectable a factor of 10 fainter, partly because of our high sensitivity and partly because of the excellent flat-fielding afforded by TDI scanning.
Besides galaxy magnitudes, the photometric survey will provide the largest and most homogeneous multicolor photometry of galaxies and stars by far. The uses of a multicolor survey include: 1) Eliminate an important bias due to the K-correction; 2) Use color as a substitute for morphology at larger redshifts to determine what types of galaxies are being measured; 3) Determine redshifts of faint galaxies using multicolor photometry (Connolly et al. 1995) Provide color information for a low-redshift sample of galaxies that can be used for comparison with high-redshift galaxies to study their evolution; 5) Identify QSOs via their color; 6) Identify many interesting classes of stars, including evolved Population II objects, white dwarfs, subdwarfs, very hot stars, carbon stars, and (dare we say?) very cool objects on the main sequence and below; 7) Calibrate Galactic extinction via its effect on the colors of stars, galaxies, and QSOs; 8) Discover previously unknown classes of objects by their colors; 9) Do optical identification and photometry of objects drawn from catalogs in other wavebands (X-ray, radio).
The spectroscopic survey is specified by the selection procedure: the angular sky coverage; nature of the sampling (e.g. filled versus unfilled); minimum fiber separation; and details of the spectroscopy (wavelength coverage, resolution, minimum signal-to-noise ratio, fiber diameter, number of object fibers, number of sky fibers). The various choices depend upon the program objectives: one would use a different strategy if the objective were to collect the largest number of redshifts than if the objective were, say, to measure the galaxy clustering correlation length to the highest precision. Our goal is to allow the greatest range of analyses to be carried out with the spectroscopic sample, and thus we plan to observe complete, filled, well-defined sample. While this is perhaps not the most useful or efficient observing strategy for some specific analysis, is likely to provide the best sample overall for understanding the structure in detail, the relationship of galaxy morphology with that structure, and certainly for understanding almost all dynamical aspects of the structure. Of course, as our scientific goals include measuring clustering on the largest scales, we do put great emphasis on making the spectroscopic selection as uniform as possible, in a way that allows the selection function with respect to redshift to be measured in as model-independent a way as possible.
The remainder of this section gives a general outline of how one might approach the optimum strategy. The principal conclusions are:
Is it worthwhile to go fainter than about r' = 18.2 ? Some elementary considerations might suggest yes. If we measure galaxies to a limiting brightness s , then the exposure time tau needed to reach some fiducial signal-to-noise ratio varies as tau ~ s-1 (if the sky background is negligible), but the number of galaxies varies as N ~ s-1.25 . Hence the number of galaxies that can be measured in a fixed length of time varies as N ~ s-0.25 . Thus, even though the exposure times are longer for fainter sources, we can more than compensate by stuffing more fibers into the focal plane. Nevertheless, several competing factors make it undesirable to go much fainter, and the evaluation of the optimum limiting magnitude is relatively complex.
The main limit on going fainter is competition from the sky background. The dark night sky at our site has a measured V -band surface brightness of about 21.7 mag arcsecond -2 , or about 21.2 in our r' band. For point sources, the optimum limiting magnitude in the sense discussed above comes approximately where the sky and object contribute equally. The optimum fiber diameter for very faint stars (i.e., the size that maximizes the signal-to-noise ratio) is about 1.5 times the seeing full width at half-maximum. If we want to work in seeing as bad as 1.5 arcseconds, the fiber diameter should be at least 3 arcseconds. (For extended sources, the optimum diameter is larger.) The sky intensity within an area of 3 arcseconds diameter is equivalent to the light from a r' = 19.1 star. Since 65% of the light from a star enters the fiber with this seeing, the limit for stellar objects is about r' = 18.6 . For point sources, the time required to reach a given signal-to-noise ratio for a source of flux s changes rather abruptly from a s-1 relation to a s-2 one at this brightness level.
The case for extended objects is more complicated. A characteristic break point in efficiency again occurs where the light from a galaxy is comparable to the night sky. For a representative low surface brightness spiral, this occurs at about r' = 18 , or perhaps a little fainter. The change is not so abrupt, and the inefficiency as one goes fainter is compensated to some extent for extended objects since the fainter ones are smaller and one gets an increasing fraction of the flux into the aperture. At a cutoff of about 18 in r' the flux fraction grows something like s-1/2 , so a tau ~ s-1 behavior is also applicable to objects fainter than the sky. Of course, the same considerations apply for bright objects, and one does not do nearly as well for bright objects as the s-1 relation would suggest. Our combination of r' magnitude and surface brightness cuts yields a sample with a sharp cut-off in light down the 3" fiber at 19.5, which is only a few tenths of a magnitude fainter than the light from the sky.
Other factors argue against going much fainter than r' = 18.2 . First, even at that magnitude, the number of fibers needed in the telescope field is of order 600 and management of that many fibers will be a challenge. Second, as will be shown below, exposure times are still quite long. Third, although the most efficient survey in some particular sense might be one that is narrow-angle but deep, in that case most information on large-scale structure will be derived from objects that are relatively faint and therefore difficult to study in other ways. Fourth, unless the survey covers a large solid angle, the largest linear dimension is along the line-of-sight for which information on correlation functions is more difficult to interpret because of the wide range of galaxy luminosities, and the inevitable aliasing, or crosstalk, between the survey volume and the structures within it (e.g., Kaiser & Peacock 1991). Finally, and perhaps technically most important, the subtraction of the sky spectra is easy when the sky and object are comparable and we can get by with relatively few (we are considering a number like 20) sky fibers, while if we go much fainter the problem becomes very much harder, and at the faintest levels we might be driven to use one sky fiber for each object fiber and chopping, which is used for the Norris spectrograph at Palomar (although many workers do not need large numbers of sky fibers even when doing very faint object spectroscopy; cf. Wyse and Gilmore 1992).
Does it pay to carry out an unfilled survey? There are two possible strategies. First, one might observe galaxies in noncontiguous fields. One might have gaps of order the telescope field diameter of 3°, in which case the corresponding linear gaps are of order 16 h-1 Mpc at z=0.1 , roughly the distance scale over which we are trying to measure structure. A second possibility is that if one were restricted by the number of fibers that could be placed in each field, then one could observe only every second or third galaxy. The main effect of incomplete sampling is that we lose information on the smallest scales, and in particular we will be less able to identify poor clusters, groups, and pairs for mass studies. With our proposed dense-sampling strategy, we are limited only by the finite number of galaxies, and since we are firmly of the opinion that the best statistical methods for analyzing the structure have yet to be invented, it is worth preserving as much detail as possible. The suggested volume is roughly 3 x 107 h-3 Mpc³, or about 2000 30 Mpc `bubble' volumes, so if correlations are weak or absent on larger scales, many statistical questions can be answered at the 2% level or so.
A good starting point for choosing the spectral resolution is the Center for Astrophysics redshift survey (Tonry and Davis 1979). Spectra from that survey cover 4300 - 6900 Å with a resolution of about 5Å (1.8Å per pixel). The spectrograph does not have good blue sensitivity. Redshifts are determined either from absorption lines or emission lines -- in both cases only a few lines contribute most of the signal. In absorption, three features are dominant: the Mg triplet lambda 5180, Ca lambda 5270, and the Na I doublet lambda 5890. In emission, H alpha is the strongest (and often the only) line. The strongest lines blueward of the sensitivity limit at zero redshift are the Ca II K and H lines at 3933, 3969Å and the G band 4300Å in absorption, and [OII] 3727Å in emission.
The spectral sampling is set by the requirement that broadened absorption lines be well resolved. Although there is a large range in galaxy velocity dispersions, most of the objects in the survey will be moderately luminous galaxies (typically spirals). Nearby spirals like M31 have velocity dispersions that range from 100 to 150 km/s, and we will take 125 km/s as a working value, which corresponds to 5.1Å full width at half-maximum at a central wavelength of 5200Å. Given a finite number of pixels available and the reality of read noise for CCDs, the best resolution is that at which these lines are just resolved. Lower resolution reduces the signal-to-noise ratio because the lines are diluted with continuum light; higher resolution limits the spectral range and hence the number of lines available for velocity and dispersion measurements. Our spectrographs (see Chapter 7) will have a 3 Å projected aperture width which resolves 5.1 Å and fully samples a line with 6 Å FWHM, and does so with 3 pixels per resolution element on the CCD.
A spectral range of about 5100 - 6600 Å in the galaxy rest frame covers many of the major emission and absorption lines. Significant numbers of galaxies will be detected out to a redshift of 0.25, so the upper wavelength limit should be at least 8250Å for H alpha . Alternatively, we might insist on covering [O II] lambda 3727 at z = 0 , and the range lambda lambda 3700 - 6600 , sampled at 1.4Å per pixel, would have the same velocity resolution. In particular, the absorption at H and K is so strong that it is often easier to get the redshift for a faint, high redshift object in which they appear in one's band than a brighter nearby one in which they do not. Since we will have good sensitivity in the blue, the blue cutoff should include them if possible, at least at all but the very smallest redshifts. As described in Chapter 7, we will use two double spectrographs, one side of each covering the range lambda lambda 3900 - 6100 , the other lambda lambda 5900 - 9100 , each range sampled with 2048 pixels. Thus the CaII K line lies within the range for all redshifts and lambda 3727 for redshifts larger than about 0.05.
Provided that the spectral resolution is sufficient to resolve the absorption lines, the minimum signal-to-noise ratio needed to derive a redshift depends mainly on the strength of the absorption lines. For convenience, the signal-to-noise ratio per Å of spectral continuum will be quoted. For an elliptical galaxy with strong lines, spectra obtained in the Center for Astrophysics redshift survey show that one can measure a reliable redshift if the signal-to-noise ratio per Å is at least 8, i.e., one needs to collect 64 object photons Å-1 assuming that the noise is dominated by photon statistics from the source. This number must be increased, however, if sky background and/or readout noise is significant. A big problem for some galaxies is that they have weak absorption lines (presumably because they have a significant amount of light from early-type stars) and yet do not have strong H alpha emission. In these cases one may need 2 or 3 times as many photons to derive an absorption-line redshift. We adopt as a guide the goal of obtaining spectra with S/N of 15 per Å. Simulated galaxy and quasar spectra and the sensitivity estimates in Chapter 7 indicate that we can in fact reach this goal with exposures of somewhat less than a one hour with our telescope and spectrographs.
The 3° field is big enough that differential refraction effects across it are serious, and the 3-arcsecond fibers small enough that chromatic differential refraction is serious. The observing strategy must cope with these issues, and we must resolve at the outset whether they are so serious that we cannot proceed.
With our choice of survey area, and the (probably reasonable) requirement that fields along the Southern and Northern survey borders are taken at meridian crossing, the minimum altitude reached is 34.5deg ( +- 30m hour angle). The difference in position between an image at 4000Å and one at 9000Å at that altitude is 1.9 arcseconds for the mean atmospheric conditions at Apache Point. The center of the image over this band is at about 5100Å, independent of altitude. In comparison, at an altitude of 25°, the lowest if we had used the b > 30° region, the difference is 2.9 arcseconds, almost the full diameter of the fiber. The flux loss when a typical faint galaxy image is displaced by 1 arcsecond in a 3 arcsecond fiber has been investigated in the simulations and ranges from 7 to 20%. A starlike object loses about 16% for a similar displacement in 1 arcsecond seeing, and 20% in 3 arcsecond seeing; the numbers for galaxies are not very sensitive to the seeing. The displacement goes roughly like 1/ lambda² - 1/ lambdac² . Thus the spectrum for an image centered on the fiber at 5100Å is multiplied by a function which looks like
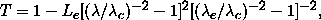
where Le is the loss fraction at the ends, and lambdac is the central wavelength in the sense that the displacement at the ends is symmetric with respect to it; lambdae is the wavelength at either end. The average loss over the spectrum is about a third of the loss at the ends, but that may or may not be reassuring depending on where the strong spectral features are on which one is basing the redshift.
The situation is actually not too bad for galaxies; at the redshifts where bright galaxies are dropping out of the sample, about 0.2, H and K are near 5000Å where the losses are smallest; even lambda 3727, having only lately entered the range, is in a place where the losses are about 24% of those at the ends. H alpha does not fare so well, and is at a place where the losses are 80% of those at the ends at this redshift, but at zero redshift, the loss is only 25% of the end losses, and we will be called upon to use H alpha mostly for low-redshift dwarfs (which also tend to be large on the sky, so the end losses are small.) All in all, the average loss, which varies between 3% and 7%, is something we can live with. The effect as a signal loss is small compared to the increase in sky brightness at this altitude, which is 1.45 times brighter in the continuum than the sky at 1.2 airmasses where the simulations were made, and will require 22% longer exposures to reach the same signal-to noise ratio if the galaxy and sky contributions are about equal. The argument can be made that we should increase the exposure times by of order 25% at these low altitudes if we wish to keep the survey as homogeneous as possible. It is at these same places near the boundaries of the survey where the Galactic absorption is highest, so the problem gets even worse. We discuss this problem in the next section.
A possibility that we are strongly considering is to take 4 very short (one minute) "auxiliary" spectra for every plate, with the telescope offset +- 1.5 arcsecond (a fiber radius) in directions that correspond to the altitude and azimuth in the middle of the exposure. If the very low-level vertical charge-transfer efficiency of the spectroscopic CCDs is high enough (the single-pixel signal is only a few electrons), we can bin the data on the chip into, say, 10 bins of 200 pixels each, which would have higher signal than in a single line in the full exposure. This would allow us to reconstruct in some detail the effect of chromatic differential refraction on the spectrum, and would require only about 5 minutes of overhead. One could also use this information to check the accuracy of the astrometry and plate drilling. Even if we cut the exposure time by that much, the increased information would probably be worth the small hit in the signal-to-noise ratio, and may allow us to do spectrophotometry at the level of 5% accuracy.
An effect about which we can do almost nothing is the fact that the spectra of extended objects is different in different places, and the fiber looks at different places at different wavelengths. To the extent that this affects the continuum the procedure outlined in the previous paragraph will serve, but not for differences in the strengths of features on the scale of the wavelength resolution.
The other effect of differential refraction is that the images of objects move relative to one another as the exposure progresses, and, of course, the mean positions depend on the mean hour angle. With a spectroscopic field center at an altitude of 36.5° on the N-S boundaries of the survey, the refraction difference from the top of the field to the bottom is 8.1", in the sense that the image is compressed with respect to the sky. The image is also compressed laterally because it is higher in the sky, but the effect is smaller, 2.7" (the ratio is the square of the sine of the altitude, so near the zenith refraction results in a change of scale alone.) We can adjust the scale of the image at the telescope in real time, but if we drill the plate neglecting refraction the errors are too large; for the mean scale, corresponding to a shrinkage of 5.4 arcseconds in 3 degrees, the images are as much as 2.7 arcseconds from the fiber centers, a disastrous difference. Thus one must assume an hour angle, calculate the refraction, and drill the plate to suit. In the course of an hour exposure, the refraction changes (most importantly, the refraction pattern rotates with respect to the field) and at 35° altitude the maximum image motion going from the meridian to an hour over, assuming that the exposure is guided in the middle of the field and the rotation is controlled to minimize the error at the edge, is about 0.8 arcseconds. It is a little less if one starts 30 minutes east and goes to 30 minutes west, but not much. Thus if one drills the plate for the mean position, the errors are at most 0.4 arcsecond, about 24 microns. The scale can be adjusted to make the maximum vertical component of the error about half that. (We obviously care most about the vertical component because the error is there compounding the chromatic effects). The effect of this on the spectra is very small, and corresponds to a seeing degradation of about 0.13 arcsecond in the root-sum-square sense (i.e. going from 1.0 to 1.01 arcseconds.) Horizontally, one gets essentially the full effect, but this is equivalent to 0.26 arcsecond added in quadrature with the seeing, or going from 1" to 1.03" . We are in this happy position only if the plate is drilled for the hour angle range actually used, and if the drilling tolerances are smaller than these errors. Happily, the latter seems to be possible, but the former requires very careful scheduling.
There are very compelling reasons to attempt to make a survey which is as homogeneous as possible outside the Galaxy, i.e. one in which the reddening-corrected limit is at least roughly constant over the survey area. The average color excess at the boundaries of the survey is about 0.08 magnitude, but varies widely. Our photometric survey will itself produce the best reddening and extinction data which have ever been obtained. It is unfortunately not going to be possible to measure the effects of reddening in the photometric survey on a timescale short enough to be able to use this in spectroscopic target selection. Indeed, we plan to measure reddening using hot stars. We will need to obtain spectra of these stars in order to confirm their spectral types, which means that we will not be able to measure the reddening until the spectroscopy has been done. Therefore we will correct our object catalogs for reddening following Burstein and Heiles (1978) or updates, such as the DIRBE maps (following Schlegel 1995).
There will be in the survey area about 4000 hot white dwarfs and O and B subdwarfs brighter than g'=20.5 , which can be distinguished by their colors and which will yield individual accurate reddening values, and a like number of cooler but still useful horizontal branch stars. There will be more than a million F and G subdwarfs, a hundred per square degree, which will be useful at least statistically, and, of course, the galaxy counts themselves, which will go deep enough that several almost independent samples (from the point of view of spatial clustering statistics) can be chosen at different brightness levels. The color distribution of faint galaxies can also be used to measure the reddening.
If one is to compensate for extinction which dims an object by a factor f and attempt to reach the same signal-to-noise ratio as for an object with no extinction, the exposure time is increased by a factor between f-1 for very bright objects and f-2 for faint ones, all other things being equal. If the extinction over the survey region goes roughly as the secant of some equivalent latitude, then a very crude representation of the correct exposure time for faint objects, including the effects of both extinction and sky brightness, referenced to the exposure time at the zenith at the survey center, is something like
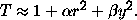
Where
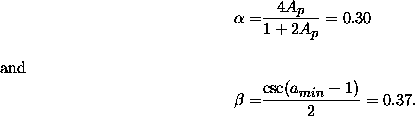
Here r is the angular radius of the point in question from the survey center in units of the radius to the boundary in that direction, y is the angular distance of the point from the survey equator in units of the total survey latitude extent, Ap is the Galactic extinction near the pole, and amin is the minimum altitude at the survey boundary. The first correction term represents the effect of Galactic extinction, the second the brightening of the night sky. This assumes that the exposure is done at small hour angle, and is calculated for a galaxy at the survey limit where the total galaxy signal is, at the zenith, about equal to that of the sky. The values given are for our proposed survey geometry. The mean value of T over the survey region is about 1.25, and at the northern and southern boundaries near the central meridian of the survey is about 1.65, which represents essentially the full dynamic range of the exposure times. Thus near the survey center, presumed done near the zenith, the exposure time should be 20% smaller than mean, and near the boundaries on the survey meridian 32% longer; the limiting magnitude, however calculated, should be adjusted faintward by an amount equal to the Galactic extinction in the relevant waveband.
It is important to note that even if the model one uses for the absorption is not correct in detail, these corrections will help and should be applied. One can correct for residual effects in large-scale structure analyses by means of the selection function, but the smaller the corrections the smaller the remaining systematic uncertainties they leave behind. There need be no guesswork at all about the sky brightness correction, since it is monitored continuously by the guiding system (cf. Chapter 7).
We plan to operate the survey instrument and software for one year to test all systems thoroughly before actually beginning the survey. This is an expensive proposition, but we consider it absolutely necessary for several reasons.
The value of the survey will be severely compromised if it is not homogeneous, so we feel it imperative that insofar as possible, nothing be changed that influences the data quality once the survey is underway. For a system this complex, it seems inevitable that there will be troubles and inefficiencies which need fixing, and a year seems a reasonable timescale to accomplish this. There are several aspects about which we are particularly concerned, which include:
Details of the performance of the camera system, which include tracking algorithms, the scale-determining algorithms discussed in Chapters 5 and 7, ghost images, the effects of stars bright enough to saturate the CCDs, the focus servo, and others which will arise as engineering is completed.
Photometric and astrometric calibration. The former will require the setup of a network of either photometric or spectrophotometric standards before the survey begins (for this reason we plan the monitor telescope to go into operation even well before the test year), and we must test in detail the rather unconventional approach to calibration proposed here (Chapter 5). The astrometry can be refined as we progress in the survey, but we must know that it is good enough at the beginning that the errors have negligible effect on the placement of the spectroscopic fibers. The photometry must be good enough that there is negligible effect on the selection of the spectroscopic sample.
All the detailed algorithms which make up the pipelines with which we are reducing the data need to be tested with real data. We have made out extensive simulations of the SDSS data with the express purpose of testing these algorithms (cf. Chapter 9), but there are sure to be any number of senses in which these simulations are not realistic enough to test the pipelines thoroughly.
The selection criteria for galaxies for the spectroscopic sample must be thoroughly tested on real survey imaging data, and the statistics appropriate to the sample investigated. This is perhaps the most serious algorithmic problem we must address during the test year, and the one thing we must not under any circumstances change once we are underway.
The selection criteria for QSOs must be similarly tested; this is in a sense a more difficult problem, since the selection criteria are designed to separate stars from QSOs in a statistical sense, and one must balance the need for a homogeneous survey in the face of a position-dependent star-to-QSO ratio (and a position-dependent stellar population), which is certain to have a large impact on the success rate of QSO selection, against the need for an efficient classifier.
The survey time to completion depends on a number of factors over which we have some control, such as the efficiency with which we can change spectroscopic plates, and switch observing modes when conditions dictate. We will learn from experience during the test year how to observe with as little overhead as possible.
The telescope instrumentation has been designed so that switching between the photometric and spectroscopic programs can be accomplished quickly during a night. The photometric program will place much greater demands on the quality of observing conditions: we expect to operate the camera only during clear, moonless periods with seeing better than one arcsecond. Since one of the functions of the photometric program is to identify galaxies for the spectroscopic observations, it is necessary that the imaging survey always be in the lead as far as sky coverage is concerned.
A 130° strip is covered at the sidereal rate in 8.6 hours, and the total scanning time to cover the whole survey field once is about 700 hours. There are approximately 1800 spectroscopic fields in the survey area. With 45 minutes of exposure time, we estimate that it will require a bit more than an hour per setting with all the overheads; then the spectroscopy alone will require about 2000 hours. The right ascension range of the survey is about 10 hours, with the extremes at pretty high declination, so we can work easily 2 hours over and perhaps three. Thus we can work about 60% of the year. If we assume that 50% of all nights are spectroscopically clear, 60% of the time on those nights is sufficiently dark (clearly a nearly-new moon low in the sky is not a problem), on 60% of those nights the survey region is accessible, and that there are 8 hours per night, we find that we can work 535 hours per year. The spectroscopic survey will thus take about 3.7 years, and the photometric survey about 1.3 years, for a total of 5 years.
The elliptical region suggested above has two more advantages from the point of view of hastening the completion of the survey. It is clearly advantageous insofar as time-to-completion is concerned to limit declination coverage and increase right ascension coverage, because at any time of the year one must thereby do less and has longer to do it; thus the elliptical region will require about 10% less time than a circular one of the same area centered at the same place. In addition, the move to earlier right ascension is a move to longer nights at a given limiting hour angle. We may well wish to cover a somewhat larger area with the imaging than the one in which we plan to do spectroscopy, precisely to check the reddening; this will also help with the tiling (see Chapter 8).
It is implicit in the discussion above that the telescope be operating nearly all the time; there are certainly a few nights around full moon when there is no time when it is dark, but in general the survey must operate whenever the sky is dark for long enough for anything useful to be done. In addition, we will see in the following section that, at least at the beginning of the survey, we will be able to go directly from the Northern survey discussed above to the deep Southern survey with no idle time. This will change as the survey progresses, because the declination extent of the Northern survey at the right ascension extremes is small, and as those areas are finished, the hour angle gap between the Northern and the Southern regions will grow too large to bridge. This has negligible effect on the time estimates above, but will open the possibility of other projects during those times.
The presence of only a small amount of moonlight will necessitate stopping operation, but we anticipate that some `bright time' will be used at the beginning for calibration exercises (letting the Monitor Telescope catch up with the secondary star patches) and consistency checks on the photometry. Another bright time exercise will be to make scans perpendicular to the great circles, to tie the photometric and astrometric systems together by more than the (relatively small) overlaps between stripes. The need for this time will ease considerably as the survey progresses.
In the autumn the North Galactic cap is inaccessible, but a substantial fraction of the South Galactic cap is visible. In principle, the primary survey strategy could be employed in the South, but this involves a relatively small augmentation of the data base. We prefer the option of a deep survey in a smaller area; this provides new and complementary scientific opportunities. Perhaps as important as the considerably greater depth is the opportunity to investigate time-variable phenomena thoroughly.
A deep survey is most efficiently done in a single, long, thin stripe. The Southern imaging survey consists of two interlaced areas that are repeatedly scanned. These scans will be co-added to produce a single, deeper image, and differences between scans will be used to identify variable objects. For example, if the survey is centered on the celestial equator and restricted to regions with less than 0.1 magnitudes of reddening, then we can go from about 20h 40m to about 5h 0m , a total of about 125°, or 8.3 hours scanning time. However, our first priority is the survey in the North, and thus we will observe in the South only in the time that none of the Northern survey area is available. This restricts us to a total of 90°, or 6 hours scanning time. The stripe is covered completely, therefore, in two strips, 12 hours.
The total area of this stripe is 225 deg² . The time per year available to it (assuming a 70-30 split with the Northern survey) is 260 hours, with the same ground rules as used above. If we devote a somewhat larger fraction of the time to imaging, say 40%, we will have about 540 hours over five years, covering the field about 45 times and obtaining a limiting flux 2m fainter than that of the Northern survey. The corresponding 5:1 limiting magnitudes are 24.4, 25.3, 25.1 24.4, and 22.9 in u' , g' , r' , i' , and z' . This schedule makes the mean interval between scans during the season about 20 days, but these will, of course, be concentrated into the dark half of the month and into stretches of good weather. The opportunity to discover supernovae and other variable objects at hitherto unexplored brightness levels is superb (see below), and we may well want to increase the fraction of time devoted to imaging still further in order to improve time coverage, even though the data in some of the extra scans might be of lower quality. A given field will occasionally be observed off-meridian, so as to break up aliasing in searches for periodic variability. Also, for many variable objects one can profitably squeeze the moon a bit, since the r' band is not too badly affected by a little moonlight, and i' and z' can stand a great deal. It is also the case that light cloud cover can be accommodated, since we do not depend on a single pass for photometry; the ability to calibrate scans in less-than-photometric transparency to scans obtained under photometric conditions is the most important factor in allowing us to increase the fraction of imaging time in the South.
The Southern survey has other practical advantages. Since the great circle for its (single) stripe is the celestial equator, the telescope can be parked and act as a transit instrument, which will result in increased stability and superb astrometric accuracy. This, combined with the long-term multiple coverage, will produce a large volume of excellent proper-motion data. In addition, the wide range in right ascension means that much of the spectroscopy can be performed near the meridian.
Finally, we will obtain photometry and galaxy spectroscopy (using the same selection criteria as in the North) in two further stripes in the South (a single pass each), along the great circles that go through alpha = 0h, delta = +15° and alpha = 0h, delta = -10°. The addition of these two stripes greatly increases the number of independent baselines of the largest extent, which will be of great use in measuring structure on the largest scales.
Although there certainly exist photometric surveys which go as deep or deeper than the Southern survey proposed here, there is no survey in existence or planned which goes so deep over so large an area of sky, nor are there any over any appreciable area with accurate five-color photometry. We view this survey as an indispensable bridge between the Northern shallow survey and the very deep pencil-beam surveys which will be possible with the new generation of very large telescopes and which go two magnitudes deeper yet.
The principal scientific drivers for a deep, multi-color imaging survey are a search for high-redshift clusters (to z > 1 ), and a characterization of the faint galaxy population, in order to probe the local population of very low luminosity and very low surface brightness galaxies and to study the evolution of galaxies and galaxy clustering. Object identifications can be made from radio and X-ray catalogs; often the most dramatic objects in these bands turn out to have optical counterparts at 24th magnitude and fainter. With the multiple exposures, variability studies will be done at brighter magnitudes. Variability will bring to light classes of AGNs and QSOs that would not be distinguished by their colors alone. Moreover, characterization of the variability of AGNs has much to teach us about the geometry of the broad-line region. Variable stars will also be discovered in this survey in great numbers, at quite faint magnitudes, although the SDSS will not compete with surveys such as MACHO and OGLE for stars brighter than 19th magnitude. Five years is long enough, and our astrometry will be good enough, that we will be able to measure proper motions for large numbers of stars (including perhaps faint nearby stars with very high proper motions, hundreds of milli-arcsec/year). Finally, this survey will undoubtedly uncover large numbers of supernovae (we conservatively estimate a minimum of 35 per observing season), allowing us to characterize the statistical properties of supernovae quite well, in particular the rate of supernovae in various types of galaxies. If we can reduce the data on a short enough time scale (see below), we can let the community know about those that are discovered, for intensive follow-up on other telescopes.
For the spectroscopic time in the South, we envision a combination of several projects; the following are some examples. The number density of quasars on the sky is ~ 240 per spectroscopic field to r' = 19.5 (i.e. one magnitude fainter than the nominal limit of the quasar survey in the North). We can indeed push the spectroscopy to these fainter magnitude because quasars, as emission-line objects, do not require the signal-to-noise ratio to get a redshift that an absorption-line galaxy requires. We estimate that two hours will be required per field to go this deep, probably broken into two one-hour exposures on different nights to minimize refraction effects. This survey will be invaluable for studying large-scale structure in the quasar distribution. By going deeper in magnitude, we probably will not substantially increase the redshift out to which quasars are seen (indeed, quasars are being discovered now at z > 4 that easily pass the Northern spectroscopic survey limits), but we will increase the sampling of the quasar density field, and denser sampling allows much more detailed characterization of clustering. In addition, this faint quasar survey will substantially extend the dynamic range for studies of the evolution of the quasar luminosity function, and it will provide information about faint peculiar stars and compact galaxies, which will inevitably find their way into the spectroscopic target list.
This survey of faint QSO candidates occupies only ~ 1/2 the fibers for a total of ~ 50 spectroscopic fields, leaving a large amount of time for other spectroscopic projects. One possibility is to target very blue galaxies appreciably fainter than the galaxy spectroscopic limit in the North; the fraction of galaxies with strong emission lines is quite high if one chooses blue enough objects. Another way to think about spectroscopy in the South is to realize that in the entire Southern stripe, there are roughly 440,000 objects (stars, galaxies and quasars) with 3" aperture magnitude brighter than 19.5 in r' . This is of the same order of magnitude as the total number of objects we could target spectroscopically in the time allowed (assuming that we keep to the 45-minute exposure times per object used in the North). This suggests that we observe all of these objects spectroscopically; this project would encompass essentially all spectroscopic projects envisioned for the South. It would prove to be a tremendous boon for studies of stellar populations in our own Galaxy, and is bound to turn up all sorts of interesting and unexpected serendipitous objects. It will be absolutely invaluable for understanding the consequences of our selection criteria for quasars, and will allow us to probe in detail how well our star-galaxy separator works (and explore the population of compact galaxies in a way the Northern survey will be unable to do). There is no reason to do this survey of roughly 400,000 objects in a contiguous stripe, of course, and considerations of Galactic structure studies will probably drive us to spread the fields between the three Southern stripes which will be surveyed photometrically (as mentioned above, we still have to survey the two "outrigger" stripes spectroscopically using the same criteria as in the Northern survey).
The strategy of the Southern survey is much more flexible than that of the Northern survey. We do not need to use the same strategy from one year to the next, and we can imagine using the telescope in a variety of ways to address specific scientific problems. It might be worthwhile, for example, to devote a few hours of imaging time to a complete photometric map of M31.
Complete analysis of the Southern photometric data will require two pieces of rather tricky software which are not necessary for the Northern survey: co-adding of frames to go deep, and subtraction of frames in order to uncover faint variable objects. However, the results of addition and subtraction analyses are not needed to select spectroscopic targets: all of the spectroscopic targets will be chosen on the basis of photometry reduced exactly as it is in the North. Searches for variable objects suitable for spectroscopy can be done quite effectively at the catalog level, and do not require the much more sophisticated frame subtraction software. Our plan is to start the Southern survey with the same data reduction software that will be in place for the Northern data; no additional software will be needed to run the Southern survey (it should be mentioned that running this survey over repeated scans of the same area is a wonderful test of the robustness of our algorithms, although we hope to find any obvious deficiencies in our algorithms during the test year). As the survey progresses, we will develop and refine the frame addition and subtraction software, which will allow us to exploit the full potential of the Southern data. Because nearly all of the Southern spectroscopic targets will be selected on the basis of the first photometric scan, the turn-around requirements on data processing are much less severe than they are in the North. However, it is clearly valuable to have fast turn-around so that we can notify the world at large about interesting transient phenomena, in time for follow-up observations. Our standard data reduction system should typically allow turn-around in a week or less. For supernovae one would ideally like to have even faster analysis, preferably on the mountain. We are not actively working to develop such capability, but we will provide a "Y-fork" on the data acquisition system so that a group with the hardware and software resources to carry out such an analysis can connect to the data stream.
Burstein, D., & Heiles, C., 1978, Ap. J. 225, 40.
Connolly, A.J., Csabai, I., Szalay, A.S., Koo, D.C., Kron, R.G., & Munn, J.A. 1995, AJ 110, 2655.
Heiles, C., 1976, Ap. J. 204, 379.
Heiles, C., 1975, Astron. and Ap. Suppl 20, 37.
Impey, C., & G. Bothun, 1989, Ap. J. 341, 89.
Kaiser, N., & Peacock, J. A. 1991, ApJ 379, 482.
Kent, S., 1985, Ap. J. Suppl. 59, 115.
Kent, S. 1996, "Defining the Northern Survey Area", SDSS Internal Memo.
Schlegel, D. 1995, PhD Thesis, University of California.
Schneider, D., M. Schmidt, & J. Gunn, 1989, A. J. 98, 1507.
Stark, A.A., Gammie, C.F., Wilson, R.W., Bally, J., Linke, R.A., Heiles, C.E., & Hurwitz, M. 1992, ApJSuppl 79, 77.
Thuan, T. X., & J. Gunn, 1976, P. A. S. P. 88, 543.
Tonry, J., & M. Davis, 1979, A. J. 84, 1511.
Wyse, R. F. G., & Gilmore, G. 1992, M.N.R.A.S. 257, 1