While wide-field optical designs exist for such focal ratios (the Baker-Paul three-mirror design, for example, and more recent variants, and the Schmidt, of course) they all suffer from either excessive length for a 2.5 meter aperture or an inaccessible focal plane, which renders the fiber spectroscopy difficult. Early design efforts revealed that there appeared to be some hope (which we realize below) that a more-or-less conventional Ritchey-Chrétien-like optical system would deliver the requisite performance while working with a focal ratio about f/5, which we need to match our chosen detectors.
After quite extensive exploration, it was determined that the CCD division of Tektronix was the only viable supplier for focal plane arrays which satisfied the requirements for quantity, large format, and broadband sensitivity. After our contract with Tektronix was well under way, an independent entity, Scientific Imaging Technologies (SITe), purchased the CCD division and its contracts. The need for good ultraviolet response dictated the use of thinned backside-treated devices; the UV fluxes are so low that very low readout noise was also required. With 24 micron pixels, the SITe devices provide excellent focal plane image sampling at about f/5 with our expected image size of about 1 arcsecond FWHM. This combination yields 0.4 arcsecond pixels, about 2.5 pixels per FWHM, and about 1 percent total power in a gaussian star image beyond the Nyquist frequency.
Efficient fibers are available in diameters of 100 to 600 microns which preserve well focal ratios faster than about f/7, and which suffer hardly any degradation at focal ratios around f/5. Fibers which subtend about three arcseconds are needed to cover the bright parts of galaxies in the brightness range of interest. The scale at f/5, 60.6 microns per arcsecond, requires 180 micron fibers, which have excellent optical performance if handled and terminated properly and also give good sampling for the 24 micron pixels of the large Tektronix/SITe imaging arrays at the demagnified focus of the spectrographs. The focal ratio, therefore, was fixed at f/5.0.
As pointed out in the design report for the Swope and Irenée DuPont telescopes by Bowen and Vaughan (1973) it is possible to design a Ritchey-Chrétien telescope with a flat field by making the curvatures of the primary and secondary mirrors the same, which yields zero Petzval curvature in the focal plane. Since a Gascoigne astigmatism corrector is required, and since this element introduces a bit of positive field curvature, the design needs to deviate a little from this prescription, but not by very much. This results in a final focal ratio of just under twice the primary ratio, depending a little on the back focal distance, and a very large secondary, about half the primary diameter for the field sizes obtainable with f/4 primaries (about 3 degrees). For large telescopes one would like to get around the limitation of slow primaries and large secondaries. These desiderata were met in the design of the 2.5-meter DuPont telescope with the introduction of only moderate field curvature.
In addition, conventional Ritchey designs with Gascoigne correctors this fast have unacceptably large lateral color, both for this imaging application and (especially) for the fiber spectroscopy. We were therefore compelled to go to somewhat more complex systems, and have evolved a design with a two-element refracting corrector which has excellent performance. It makes use of the fact that the astigmatism correction of a Gascoigne plate goes as the square of the distance from the focal plane for a given strength, while the lateral color and distortion only go linearly. Thus a pair of plates, one of the usual form and of weak power placed some distance from the focal plane, and another the negative of the usual form of n times the strength of the first placed 1/ nth the distance of the first from the focus, can correct astigmatism while introducing no lateral color or distortion. Distortion remains at a level (12 microns over the field of the camera) set by the order of the aspheric used for the second corrector element and can in principle be removed (or specified) exactly; the lateral color is less than 10 microns peak-to-peak over the whole field over the spectral range of the spectrograph, and is a negligible contribution to the image diameter for any filter or field location in the camera.
The design presented here has almost zero distortion in the sense that the radius in the focal plane is proportional, to high accuracy, to the field angle (not its sine or tangent); zero distortion for most wide-field imaging is defined for the condition that the radius in the focal plane is proportional to the tangent of that angle, which results in faithful representations of figures on planes, but we wish as faithfully as possible to image figures on a sphere onto a surface which is almost planar. For this case a compromise is necessary between the wishes for constant scale in the sense that meridians have constant linear separation in the focal plane, and the desire that parallels of latitude do likewise. The optimum case depends somewhat on the aspect ratio of the field and is somewhere between the radius in the focal plane going like the sine of the input angle and its tangent. For a square focal plane, which is close to the situation at hand, the radius approximately proportional to the angle itself is best, and we have made this choice. The errors can be minimized by clocking different chips at different rates to correspond to the local scale along the columns, but we have chosen for reasons of noise reduction and simplicity in the data system to clock all CCDs synchronously. Our design results for the best compromise tracking rate in worst-case image smearing along the columns of 0.06 arcseconds, 3 microns, or 0.14 pixels over the imaging array. Stars do not quite follow straight trajectories in the focal plane, but this is compensated for by a slight rotation of the outer chips, amounting to about .006 degrees at the corners, and causes an error of only about 0.24 pixel if uncompensated.
The design uses a 2.5-meter f/2.25 primary with a 1.08-meter secondary, which with its baffles (1.30-meter dia.) obscures 27% of the incoming beam. The central hole in the primary is 1.17 meter in diameter. Cassegrain telescopes with fields this large are notoriously difficult to baffle, but a variant on the "Venetian blind" baffling system used in the DuPont design will work well here. The optical layout and the current baffle design is shown in Figure 2.1; the rays in that figure are for an object at the extreme edge of the 3deg field. The output f/ratio is 5.0, and the focal plane is 0.76 meters behind the vertex of the primary in order to clear the cell and allow room for the instruments. The telescope is quite short-coupled, with the secondary only 3.6 meters in front of the primary. The corrector consists of two aspheric fused quartz elements, as discussed above. The first (`Gascoigne') element is approximately coincident with the vertex of the primary mirror; there will be two interchangeable rear correctors, a very thick one associated with the camera (and in fact an intimate part of its mechanical design -- see Chapter 4), and a much thinner one for use with the spectrograph. The top surface of the second element in the camera configuration is just 58 mm from the focus, and for the camera element the back surface of the filters, which are cemented to the corrector, is 8 mm from the focus. The spectrographic configuration has 34 mm of working space behind the second corrector. The 3° field is 0.65 meters in diameter; over this field, the focal surface of the camera configuration is described to reasonable accuracy as a simple quartic in the radius; it is flat to within about +- 0.2 mm over the inner 0.5 m, and rises rapidly about 2 mm at the edge.
The CCDs for the imager will be mounted to conform to the focal surface, which requires a tilt of just under a degree at the edge of the field. There is one further complication in the design, namely that the CCDs as produced are slightly convex, with a reasonably well controlled radius of about 2.2 meters. The best fit plane results in focus errors of about 100 µ RMS, which at f/5 corresponds to an image degradation of about 20 µ. We have chosen not to live with this, but instead to correct this curvature individually for each chip with weak field flatteners cemented to the rear face of the corrector. This is more to attempt to keep the point spread functions reasonably constant over a chip than a fundamental discomfort with global focus errors this large, but we shall see that for some chips in the array there are unavoidable significant variations anyway.
The spectroscopic optical configuration is similar; the two share the primary, secondary, and Gascoigne corrector, but the last corrector is substantially different. It is much thinner (which substantially reduces longitudinal color), quite strongly curved, and a bit farther from the focal plane than the one for the camera. Its design was optimized for lateral color, which is better than 4 microns RMS over the whole field while maintaining polychromatic images better than 1 arcsecond RMS diameter. The primary-secondary spacing is also slightly different; the difference is well within the secondary focus range. The spectroscopic design violates the `telecentric' condition that the focal plane be perpendicular to the central ray in each image. This means that the fibers are not placed perpendicular to the focal plane. We will use drilled plug-plates for the fibers, and the most straightforward way to deal with the lack of telecentricity, as we shall see, is to drill the plug-plates for the fibers while the plates are deformed slightly. This will be discussed further in Section 7.6.0.1.
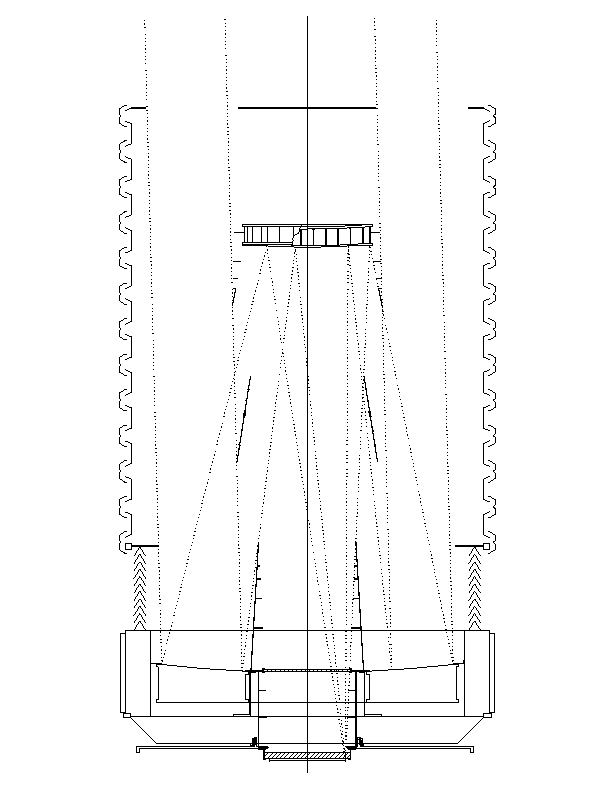
The baffles and optical layout of the SDSS telescope. The outer interlocking "C"-shaped baffles which form the upper tube are carried by an independently mounted and driven wind baffle mechanism and take the major wind loads on the telescope. The corrector system are the two thin plates close to the focal plane. The rays shown are from the edge of the 3° field.
| sur | c | s | glass | a2 | a4 | a6 | a8 | k | clr dia |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -8.889e-5 | 0.0 | -air | 0.0 | 0.0 | 3.81e-22 | -1.52e-29 | -1.285 | 2500 |
| 2 | -1.390e-4 | -3646.14 | air | 0.0 | 0.0 | 1.79e-19 | 0.0 | -11.97 | 1080 |
| 3 | 0.0 | 3621.59 | fq | 2.321e-5 | -1.173e-10 | -7.87e-17 | 1.59e-22 | 0.0 | 722 |
| 4 | 0.0 | 12.0 | air | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 721 |
| 5 | 0.0 | 714.00 | fq | -2.732e-4 | 2.056e-9 | -5.81e-15 | 1.75e-20 | 0.0 | 657 |
| 6 | 0.0 | 45.00 | bk7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 652 |
| 7 | 0.0 | 5.00 | air | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 651 |
| 8 | 0.0 | 8.00 | air | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 651 |
| sur | c | s | glass | a2 | a4 | a6 | a8 | k | clr dia |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -8.889e-5 | 0.0 | -air | 0.0 | 0.0 | 3.81e-22 | -1.52e-29 | -1.285 | 2500 |
| 2 | -1.390e-4 | -3644.46 | air | 0.0 | 0.0 | 1.79e-19 | 0.0 | -11.97 | 1080 |
| 3 | 0.0 | 3619.91 | fq | 2.321e-5 | -1.173e-10 | -7.87e-17 | 1.59e-22 | 0.0 | 722 |
| 4 | 0.0 | 12.0 | air | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 721 |
| 5 | -4.307e-4 | 672.64 | fq | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 657 |
| 6 | 0.0 | 10.00 | air | -7.747e-5 | -4.123e-10 | -6.53e-15 | 5.23e-20 | 0.0 | 656 |
| 7 | 0.0 | 86.61 | air | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 653 |
where tc is the solution to the conic surface equation
The index for fused quartz (fq) is 1.46415 at 4700 Å.
The camera design is specified in Table 2.1a, and the spectroscopic design in Table 2.1b. The primary mirror is f/2.25, and the overall system is f/5.0. In this final version, the camera design has been optimized for the chosen distribution of filters over the focal plane, and the details of the performance, and that of the spectroscopic design, are discussed below. The overall scale is 60.4 microns/arcsecond; one pixel is 0.403 arcsecond = 24 microns. There are a total of 6 glass-air surfaces, the pupil radius is 1250.00 mm with a 625 mm central obscuration, taken (not quite correctly) at the primary, and the first conjugate is at infinity.
The primary is almost hyperbolic, with about a wave and a half of 6th and 8th order flattening at the edge; the secondary is likewise, with about two waves of 6th order steepening. For interferometric tests of the primary, we used a null lens verified using a technique developed by J. Burge (Steward Observatory Mirror Lab) which uses a computer generated hologram. Interferometric testing of the secondary uses an innovative and powerful holographic test against an almost matching sphere, also conceived by Burge. The first corrector plate is straightforward, and, under contract with Contraves Inc., has been aspherized, figured and polished using a null test. The second corrector, in imaging mode, is very strong, with an aspheric sagitta of more than 8 millimeters, but the accuracy required is not very high by optical standards and the surface has been monitored with sufficient accuracy with a simple profilometer during fabrication. The contract for this second corrector plate for the camera was completed by Loomis Custom Optics with excellent results. Custom Optics also drilled the camera mounting holes (see Chapter 4) in the flat side of this corrector, and the corrector underwent application of a custom striped antireflection coating which matches the camera photometric bands. The second spectrographic corrector was aspherized, figured and polished under contract with Tinsley Laboratories.
The form of the focal surface at 4760Å is presented next, in Table 2.2b. delta is the total longitudinal focal deviation from a plane at the indicated angle, ht the height in the focal surface, lindev the deviation from a best-fit straight line relating the input angle to the height, and lin ht that linear relation. The errors (maximum of about 4 µ) simply reflect the order of the fit; it is clear that the distortion is controlled by the local slope of this surface, and can be made to vanish (or take on any reasonable form) exactly. The corrector is close enough to the focus that there is little repercussion on the image quality or the lateral color when it is modified slightly.
To discuss the quality of the images as accurately as possible requires a much more detailed analysis, which we summarize briefly here. The optical layout of the camera focal plane is sketched in Figure 2.2, which shows the locations of the 30 2048x2048 "photometric" CCDs, the 22 2048x400 "astrometric" chips, and the two 2048x400 focus sensors. The filters u' ( lambdaeff = 3540 Å), g' ( lambdaeff = 4760 Å), r' ( lambdaeff = 6280 Å), i' ( lambdaeff = 7690 Å), and z' ( lambdaeff = 9250 Å), with which each field is identified, are fully described in Chapter 4. (The camera is right-left reflection symmetric and the lower astrometric/focus array is the mirror image of the upper array). The direction of the TDI scan is upwards in this diagram, so a given star first encounters an astrometric device, then an r' chip, then a i' chip, and so on until, 485 seconds later, it encounters the final astrometric chip. The large circle is the full 90.4 arcminute radius field. Each small circle within the CCD outlines is a point for which the system has been traced with five wavelengths chosen such that each is the mean wavelength of the corresponding quintile of the filter response; thus each has equal weight in the final image. Cemented to the flat back surface of the final corrector is the colored glass component of the filter and to that the field flattener, whose radius of curvature is chosen from a set of four which spans the requirements and on whose back surface is coated the short-pass part of the filter. The central thickness of the filter/flattener sandwich is constant at 5.00 mm.
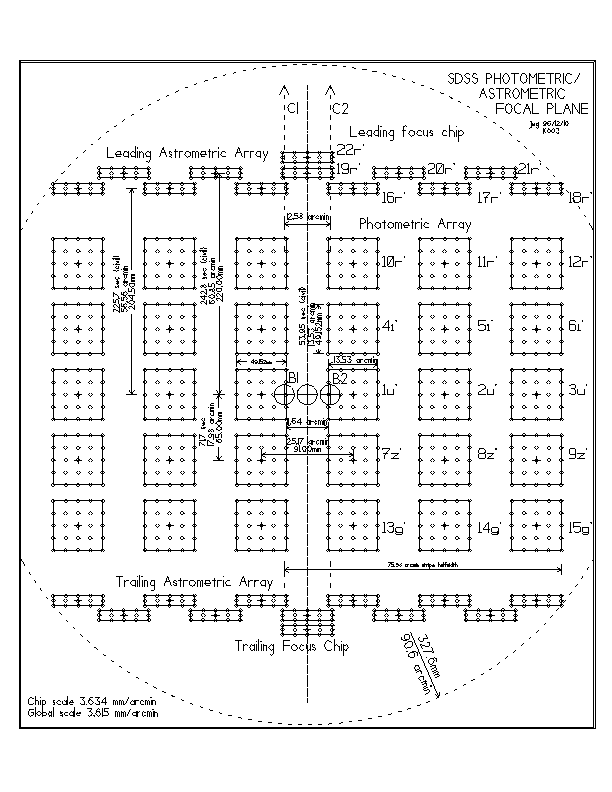
The field of the SDSS Camera. The photometric CCDs are arranged in 6 identical columns of 5 2048x 2048 chips, each with one of the five primary filter bands of the survey. Leading and trailing these columns are arrays of 12 2048x 400 chips for astrometric calibration and focus. The fields discussed in the text are identified by number and their corresponding filter. One stripe of the survey is composed of two TDI scans, one centered on the column labeled C1 through the boresight B1, the other on the column labeled C2 through B2.
The situation is summarized quantitatively in Table 2.2c, where each row lists the properties of one field (detector). The identifying numbers are as in Figure 2.2. The table lists for each field the field center in millimeters measured from the optical axis (-y is the TDI scan direction) the size of the CCD for that field, the filter, the field flattener curvature in units of 10-3mm-1 (ffc3), the CCD curvature in units of 10-4mm-1 (ccd4), the vertical scale in that field (mm/arcmin), the RMS focus error in microns over the CCD caused by mismatch between the final best focal surface and the curved CCD surface, the residual field curvature in units of 10-4 mm -1 (dc4), and the minimum (em) and maximum (eM) RMS image diameters over the field in microns. We should perhaps comment on the residual curvature; the overall scale is as listed in Table 2.2b, 3.623mm/arcmin, but the field flatteners change the scale locally for each chip to a number close to 3.6431, which was the "scan scale" -- i.e. the assumed tracking rate. Changes in this scale from chip to chip, and color to color, represent errors in the TDI images, and the field flattener curvatures are chosen for the best compromise between keeping the scale constant and matching the focal curvature. Scale errors are in general much more serious for image quality than focal errors, so there is usually some residual curvature.
The results indicate that for the photometric array, the maximum RMS image diameters are for the ultraviolet fields reaching 0.68 arcseconds for the outermost one. The increase from 27 to 41 microns from the monochromatic to the full TDI polychromatic treatment is mostly due to longitudinal color, with tiny contributions from defocus, lateral color, and substantial ones from TDI effects. Images almost as large are seen at the field extremes at the other end of the spectrum in z' , where they reach 39 microns, 0.65 arcsec RMS. The other images are of order 0.5 arcsec or better over the whole field. The problems in z' are just due to the extreme wavelength; the optimization of the system involves balancing the color effects at the wavelength extremes, and because the polychromatic effects at u' are so large the optimization was `tilted' toward the ultraviolet.
The images for the astrometric chips are almost as good except for the outer half of field 18, the outermost of the second rank of CCDs, where the images reach two-thirds of an arcsecond in RMS diameter.
Recall for all of these results that for a roughly gaussian image, the RMS diameter is 1.20 times the FWHM, so by that measure the images are correspondingly better.
The images for the focus chips (field 22) are quite good, about 0.38 arcsecond RMS diameter, and with almost no variation over the field, so even though the focus sensors (see Chapter 4 for a fuller discussion of the focusing scheme and illustrations of the focus chip images through focus) are near the outer edge of the field, there is no compromise in image quality for them. The fact that the dominant residual aberration at this point is third-order astigmatism means that the out-of-focus images are decidedly elliptical and this can be used to refine the focus servo.
Summary of Telescope Optical Performance for the Imaging Mode (k003)
| Angle | lambda | fb | h | epsilon |
|---|---|---|---|---|
| arcmin | Å | mm | mm | mm |
| 0.00 | 4760 | -0.361 | -0.000 | 0.018 |
| 30.00 | 4760 | -0.088 | -108.452 | 0.015 |
| 45.00 | 4760 | 0.052 | -162.685 | 0.013 |
| 60.00 | 4760 | -0.084 | -216.913 | 0.010 |
| 70.00 | 4760 | -0.458 | -253.069 | 0.011 |
| 73.00 | 4760 | -0.632 | -263.918 | 0.011 |
| 82.00 | 4760 | -1.380 | -296.474 | 0.015 |
| *90.00 | 4760 | -2.399 | -325.431 | 0.021 |
| 0.00 | 3540 | -0.322 | -0.000 | 0.017 |
| 30.00 | 3540 | 0.031 | -108.435 | 0.014 |
| 45.00 | 3540 | 0.267 | -162.666 | 0.013 |
| 60.00 | 3540 | 0.260 | -216.895 | 0.019 |
| 70.00 | 3540 | -0.014 | -253.053 | 0.027 |
| *73.00 | 3540 | -0.156 | -263.902 | 0.030 |
| *82.00 | 3540 | -0.803 | -296.461 | 0.037 |
| *90.00 | 3540 | -1.731 | -325.417 | 0.043 |
| 0.00 | 6280 | -0.384 | -0.000 | 0.018 |
| 30.00 | 6280 | -0.154 | -108.461 | 0.017 |
| 45.00 | 6280 | -0.065 | -162.695 | 0.017 |
| 60.00 | 6280 | -0.268 | -216.922 | 0.019 |
| 70.00 | 6280 | -0.696 | -253.077 | 0.022 |
| 73.00 | 6280 | -0.887 | -263.925 | 0.023 |
| 82.00 | 6280 | -1.687 | -296.481 | 0.029 |
| *90.00 | 6280 | -2.756 | -325.438 | 0.037 |
| 0.00 | 7690 | -0.396 | -0.000 | 0.018 |
| 30.00 | 7690 | -0.187 | -108.465 | 0.018 |
| 45.00 | 7690 | -0.124 | -162.700 | 0.020 |
| 60.00 | 7690 | -0.361 | -216.927 | 0.024 |
| 70.00 | 7690 | -0.815 | -253.081 | 0.029 |
| 73.00 | 7690 | -1.015 | -263.929 | 0.031 |
| *82.00 | 7690 | -1.841 | -296.485 | 0.038 |
| *90.00 | 7690 | -2.934 | -325.442 | 0.048 |
| 0.00 | 9250 | -0.405 | -0.000 | 0.018 |
| 30.00 | 9250 | -0.212 | -108.468 | 0.019 |
| 45.00 | 9250 | -0.168 | -162.704 | 0.022 |
| 60.00 | 9250 | -0.431 | -216.931 | 0.028 |
| 70.00 | 9250 | -0.905 | -253.084 | 0.034 |
| 73.00 | 9250 | -1.111 | -263.932 | 0.036 |
| *82.00 | 9250 | -1.957 | -296.488 | 0.045 |
| *90.00 | 9250 | -3.069 | -325.444 | 0.057 |
| Angle | delta | ht | lindev |
|---|---|---|---|
| arcmin | mm | mm | mm |
| 0.0 | -0.361 | -0.000 | -0.000 |
| 30.0 | -0.088 | -108.452 | 0.005 |
| 45.0 | 0.052 | -162.685 | 0.003 |
| 60.0 | -0.084 | -216.913 | 0.009 |
| 70.0 | -0.458 | -253.069 | 0.012 |
| 73.0 | -0.632 | -263.918 | 0.011 |
| 82.0 | -1.380 | -296.474 | -0.001 |
| 90.0 | -2.399 | -325.431 | -0.027 |
| fld | x | y | size | fil | ffc3 | ccd4 | vscl | dfoc | dc4 | em | eM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 45.5 | 0.0 | 49.2x 49.2 | u' | 1.32 | 4.3 | -3.6311 | 3 | 0.2 | 17 | 40 |
| 2 | 136.5 | 0.0 | 49.2x 49.2 | u' | 1.32 | 4.3 | -3.6326 | 10 | -0.5 | 19 | 29 |
| 3 | 227.5 | 0.0 | 49.2x 49.2 | u' | 1.32 | 4.3 | -3.6329 | 30 | -1.5 | 30 | 41 |
| 4 | 45.5 | 65.0 | 49.2x 49.2 | i' | 1.40 | 4.3 | -3.6350 | 4 | 0.2 | 18 | 21 |
| 5 | 136.5 | 65.0 | 49.2x 49.2 | i' | 1.40 | 4.3 | -3.6353 | 13 | -0.4 | 20 | 24 |
| 6 | 227.5 | 65.0 | 49.2x 49.2 | i' | 1.40 | 4.3 | -3.6339 | 30 | -1.3 | 25 | 35 |
| 7 | 45.5 | -65.0 | 49.2x 49.2 | z' | 1.40 | 4.3 | -3.6350 | 4 | 0.1 | 18 | 21 |
| 8 | 136.5 | -65.0 | 49.2x 49.2 | z' | 1.40 | 4.3 | -3.6351 | 13 | -0.5 | 20 | 26 |
| 9 | 227.5 | -65.0 | 49.2x 49.2 | z' | 1.50 | 4.3 | -3.6348 | 26 | -1.1 | 28 | 39 |
| 10 | 45.5 | 130.0 | 49.2x 49.2 | r' | 1.30 | 4.3 | -3.6342 | 12 | -0.5 | 18 | 19 |
| 11 | 136.5 | 130.0 | 49.2x 49.2 | r' | 1.30 | 4.3 | -3.6338 | 25 | -1.0 | 20 | 23 |
| 12 | 227.5 | 130.0 | 49.2x 49.2 | r' | 1.50 | 4.3 | -3.6348 | 37 | -1.4 | 27 | 32 |
| 13 | 45.5 | -130.0 | 49.2x 49.2 | g' | 1.30 | 4.3 | -3.6347 | 11 | -0.4 | 19 | 21 |
| 14 | 136.5 | -130.0 | 49.2x 49.2 | g' | 1.30 | 4.3 | -3.6344 | 24 | -0.9 | 21 | 23 |
| 15 | 227.5 | -130.0 | 49.2x 49.2 | g' | 1.40 | 4.3 | -3.6345 | 40 | -1.6 | 27 | 32 |
| 16 | 45.5 | 204.5 | 49.2x 9.6 | r' | 1.50 | 4.3 | -3.6351 | 2 | -0.1 | 19 | 21 |
| 17 | 136.5 | 204.5 | 49.2x 9.6 | r' | 1.50 | 4.3 | -3.6347 | 10 | -0.8 | 22 | 26 |
| 18 | 227.5 | 204.5 | 49.2x 9.6 | r' | 1.80 | 4.3 | -3.6358 | 20 | -1.4 | 30 | 40 |
| 19 | 0.0 | 220.0 | 49.2x 9.6 | r' | 1.50 | 4.3 | -3.6350 | 1 | -0.0 | 20 | 21 |
| 20 | 91.0 | 220.0 | 49.2x 9.6 | r' | 1.50 | 4.3 | -3.6349 | 6 | -0.4 | 21 | 24 |
| 21 | 182.0 | 220.0 | 49.2x 9.6 | r' | 1.60 | 4.3 | -3.6351 | 17 | -1.2 | 26 | 33 |
| 22 | 0.0 | 235.5 | 49.2x 9.6 | r' | 1.50 | 4.3 | -3.6350 | 1 | -0.2 | 22 | 23 |

PSFs for the SDSS camera. These are shown as produced by the optical system alone (bottom) and convolved with 0.8 arcsecond Gaussian seeing (top). Each row of five closely spaced images are from one field, with the fields from one row of CCDs arranged side-by-side. Thus the bottom three sets are from fields 13,14, and 15, and the top three, 19, 20, and 21. (See Figure 2.2). The images in a set are spaced 3 arcseconds apart.
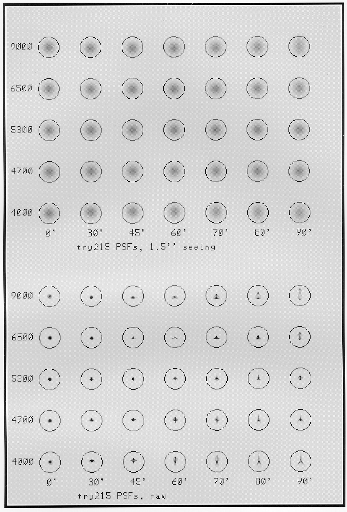
Spectroscopic PSFs for the SDSS telescope. These are as seen in the spectroscopic configuration on the mean focal surface. The field angles are (from left to right) 0, 30, 45, 60, 70, 80, and 90 arcminutes, and the wavelengths from top to bottom 4000, 4700, 5300, 6500, and 9000 Å.
Summary of Telescope Optical Performance for the Spectrographic Mode (kmg001)
| Angle | lambda | fb | h/dh | D | epsilon |
|---|---|---|---|---|---|
| arcmin | A | mm | mm | mm | mm |
| 0.00 | 5300 | -0.007 | 0.000 | 0.000 | 0.029 |
| 30.00 | 5300 | -0.143 | -108.818 | 0.000 | 0.026 |
| 45.00 | 5300 | -0.424 | -163.322 | 0.000 | 0.024 |
| 60.00 | 5300 | -0.978 | -217.855 | 0.000 | 0.025 |
| 70.00 | 5300 | -1.536 | -254.241 | 0.000 | 0.027 |
| 80.00 | 5300 | -2.265 | -290.713 | 0.000 | 0.026 |
| 90.00 | 5300 | -3.203 | -327.372 | 0.000 | 0.025 |
| 0.00 | 4000 | -0.007 | 0.000 | -0.135 | 0.036 |
| 30.00 | 4000 | -0.143 | 0.004 | -0.081 | 0.030 |
| 45.00 | 4000 | -0.424 | 0.005 | -0.015 | 0.025 |
| 60.00 | 4000 | -0.978 | 0.005 | 0.076 | 0.028 |
| 70.00 | 4000 | -1.536 | 0.004 | 0.148 | 0.036 |
| 80.00 | 4000 | -2.265 | 0.002 | 0.231 | 0.049 |
| 90.00 | 4000 | -3.203 | -0.004 | 0.325 | 0.065 |
| 0.00 | 9000 | -0.007 | 0.000 | 0.131 | 0.036 |
| 30.00 | 9000 | -0.143 | -0.004 | 0.078 | 0.029 |
| 45.00 | 9000 | -0.424 | -0.004 | 0.014 | 0.026 |
| 60.00 | 9000 | -0.978 | -0.004 | -0.074 | 0.036 |
| 70.00 | 9000 | -1.536 | -0.004 | -0.145 | 0.046 |
| 80.00 | 9000 | -2.265 | -0.002 | -0.226 | 0.056 |
| 90.00 | 9000 | -3.203 | 0.003 | -0.317 | 0.068 |
| 0.00 | 4600 | -0.007 | -0.000 | -0.058 | 0.031 |
| 30.00 | 4600 | -0.143 | 0.002 | -0.035 | 0.027 |
| 45.00 | 4600 | -0.424 | 0.002 | -0.006 | 0.024 |
| 60.00 | 4600 | -0.978 | 0.002 | 0.033 | 0.025 |
| 70.00 | 4600 | -1.536 | 0.002 | 0.065 | 0.027 |
| 80.00 | 4600 | -2.265 | 0.001 | 0.101 | 0.030 |
| 90.00 | 4600 | -3.203 | -0.001 | 0.141 | 0.035 |
| 0.00 | 6500 | -0.007 | -0.000 | 0.062 | 0.031 |
| 30.00 | 6500 | -0.143 | -0.002 | 0.037 | 0.027 |
| 45.00 | 6500 | -0.424 | -0.002 | 0.007 | 0.024 |
| 60.00 | 6500 | -0.978 | -0.002 | -0.035 | 0.029 |
| 70.00 | 6500 | -1.536 | -0.002 | -0.068 | 0.034 |
| 80.00 | 6500 | -2.265 | -0.001 | -0.106 | 0.036 |
| 90.00 | 6500 | -3.203 | 0.002 | -0.149 | 0.040 |
| Angle | Focus | ht | hlindev | yp | dyp |
|---|---|---|---|---|---|
| arcmin | mm | mm | mm | rad | rad |
| 0.0 | -0.006 | 0.000 | 0.000 | 0.0000 | 0.0000 |
| 30.0 | -0.143 | -108.818 | 0.184 | -0.0280 | -0.0247 |
| 45.0 | -0.423 | -163.322 | 0.185 | -0.0396 | -0.0324 |
| 60.0 | -0.978 | -217.855 | 0.158 | -0.0477 | -0.0347 |
| 70.0 | -1.536 | -254.241 | 0.113 | -0.0508 | -0.0329 |
| 80.0 | -2.265 | -290.713 | -0.017 | -0.0523 | -0.0293 |
| 90.0 | -3.203 | -327.372 | -0.331 | -0.0538 | -0.0258 |
In Table 2.3 data are presented which are relevant to the spectrographic mode. At each of seven field angles from the center to the extreme edge, the focal properties are given on a surface which represents the average focal surface over the spectrograph wavelength range of 3900 Å to 9200 Å (the spectrograph is described fully in Chapter 7). The first set of entries is for 5300 Å, which roughly centers the range of index variations for the spectrograph. The height differences (in the sense of the height at the given wavelength minus the height at 5300 Å, which are tabulated after the 5300 Å entries), thus represent lateral color, which is seen to be 10 microns total, +- 5 microns, or less over the whole field, and are even somewhat smaller at the edges where the images are larger. The D s are longitudinal deviations from best focus at that wavelength, and the epsilon s are RMS image diameters at the compromise focus. It is only at the wavelength extremes and at the extreme edge of the field that the RMS diameters of the compromise images exceed 1 arcsecond; the best focus images there are substantially less than 1 arcsecond (45 and 40 microns at 4000Å and 9000Å, respectively, at 90 arcminutes radius), and the increase is due solely to longitudinal color. The 72 micron worst-case RMS diameter is still much smaller than the 180 micron fibers, however, and the effect on throughput is not large; we discuss the issue more fully below. The details of the average focal surface are presented next: the sagitta of the focal surface, the mean height (here just the average of the 4000 Å height and the 9000 Å one, and presumably where one will drill the fiber hole), the deviation from a linear relation with the field angle (it is seen here that the different final corrector form, chosen to yield the best polychromatic images, results in quite serious distortion, but this is of no importance for the spectrograph), the direction cosine of the central ray measured from the direction of the axis, and the difference between this angle and the angle which the normal to the focal surface makes with the axis. This last entry is the angle with which the fiber hole must be drilled into a plate which conforms to the focal surface. The maximum value is about 2.0 degrees, compared to the 5.7 degree half-angle input cone at f/5. The losses, even into the f/4 input beam of the spectrograph, are large enough to be important, and we will compensate for it by drilling the holes into a deformed plate, as will be discussed in detail in Chapter 7.
As will be discussed further in Chapter 1, we expect to use the best-seeing time for imaging and do fiber spectroscopy under less-good conditions; average seeing for the latter will probably be in the range 1.2-1.5 arcseconds. Differential refraction at the ends of the spectrum at the maximum zenith angle (55 degrees) is just under +- 1 arcsecond from the central wavelength image at the altitude of the site. With 1.5-arcsecond Gaussian seeing, a 3-arcsecond fiber at the field edge collects 95% and 92% of the light at 4000 Å and 9000 Å, respectively, when centered on the image, and at worst 65% and 67% when decentered by 1 arcsecond. This is not substantially worse than the situation in the center of the field at the central wavelength, where the centered number is 98% and the 1-arcsecond offset number is 72%. For extended objects, we collect a smaller fraction of the light, of course, but the differential between the center and edge is smaller.
Greyscale PSFs for the field angles in the table are shown in Figure 2.4, and convolved with 1.5 arcsecond Gaussian seeing; the images are 6 arcseconds apart in the mosaic, and the circles are three arcseconds in diameter, the input diameter of the fibers.
The telescope is an altitude-azimuth design similar to the Apache Point Observatory (APO) and Wisconsin, Indiana, Yale, NOAO (WIYN) 3.5 m telescopes. (Mannery et al. 1986a,b, Gunnels 1990a, Johns and Pilachowski 1990). This design takes full advantage of lightweight mirror technology resulting in a telescope with low inertia, low friction, and mechanical simplicity.
We have elected both for cost reasons and for thermal performance to use a roll-away enclosure. The telescope is protected from the wind and stray light by means of an independently mounted and driven baffle which is coaxial with and encloses the telescope.
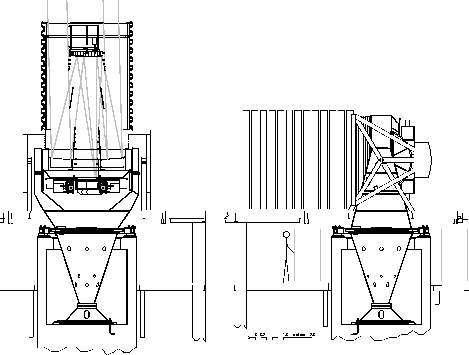
Two views of the 2.5-meter telescope. The mechanical design is essentially a scaled version of the WIYN 3.5-m instrument. The wind baffle and the light baffles are shown in relation to rays from the edge of the 3° field of view.
The eight metering elements of the secondary truss are graphite fiber reinforced epoxy tubes. This material has about 2.3 times the stiffness to mass ratio of steel. This confers the following benefits:
The moving mass of the SDSS 2.5-m telescope is 15,500 kg, which is light enough that exotic bearing technology is hardly required. We have chosen to use precision rolling-element bearings and friction drives throughout. These elements have all been manufactured and installed at the site and we have reasonably reliable measurements of the errors associated with their manufacture.
A pair of 2.54 meter diameter, hardened and ground drive segments are mounted on the sides of the PSS next to the fork. The measured high frequency (greater than eight cycles/revolution) runout of the drive segments is less than 100 nm RMS. Motor driven capstans, friction-coupled to each disk, provide balanced altitude drive torques and minimize windup of the PSS (Gunnels, 1990b).
The telescope azimuth structure consists of the fork and the azimuth cone. At the apex of the azimuth cone is a spherical roller bearing that supports the weight of the telescope. At the upper end of the cone is a 2.54 meter diameter disk, with a hardened and ground outer surface. Its high frequency runout is 220 nm RMS. This disk is guided by four roller assemblies, two of which are motor driven. These rollers, with the bearing at the cone apex, define the telescope azimuth axis.
Incremental encoders are friction coupled to the large disks. Readily available encoders (ROD 800, Heidenhain Corp., Elk Grove Village, Illinois) with a reduction ratio of 25:1 give 3.6 milliarcsecond resolution on the sky and allow slew rates higher than 4 °/s. Absolute axis encoding is provided by magnesensors (Sony Corporation, Park Ridge, New Jersey). These devices detect the position of magnets mounted to the drive disks and generate a signal repeatable to about 1 micron or better than 0.2" on the sky. Each axis is controlled by a third order dc position control system (Schier, 1990).
We have measured the dynamic performance of the APO 3.5-m telescope and find that the telescope is quite stiff with locked rotor resonance frequencies (the natural frequency of the telescope about an axis with the drive motor shafts locked) of 7.8 and 11.7 Hz for the azimuth and altitude axes respectively. Scaling laws indicate that a similar 2.5-m telescope should have 40% higher frequencies.
Rolling element bearings are used for each axis. These bearings require little maintenance, are low in friction, and generate negligible heat during operation. The measured high frequency radial run-out of the spherical roller bearing used as the lower azimuth bearing for the SDSS 2.5-m telescope is less than 310 nm RMS. This corresponds to a contribution of 23 milliarcsecond to the RMS tracking error for the telescope. The high frequency radial run-out of the altitude bearings is 51 nm RMS. They are estimated to contribute less than 6 milliarcsecond RMS tracking error.
The mirror is a borosilicate honeycomb (Figure 2.6) and was cast by Hextek Corporation (Tucson) in July 1992. The casting technique is similar to that developed at the University of Arizona Mirror Lab, except that the furnace is not rotated. The first casting attempt failed during annealing and cracks were found in the blank when the oven was opened. The causes of the failure were identified and corrected and the mirror was reheated in January. After a successful anneal, the blank was cleaned and inspected and found to be of excellent quality with low residual stresses. The Optical Sciences Center at the University of Arizona generated, figured and polished the mirror, which was delivered, aluminized, to APO in July 1996.
The primary mirror is supported on air pistons using elastomeric, low-friction rolling seals for both axial and transverse supports. Three stiff load cells serve as axial hard-points. Simple servo systems act to control the pressure provided to those air pistons in the 120° sector associated with each load cell so that the unsupported mirror weight applied to the load cell is less than 10 N. Each axial hard-point is positioned axially with a motor driven lead screw. This allows control of primary piston and tilt.
As the telescope changes elevation from zenith to horizon, the secondary will sag about 500 microns with respect to the primary optical axis. This decollimation is corrected by actively translating the secondary so that its vertex remains on the optical axis of the primary and correcting the tilt of the secondary as necessary.

Primary mirror at the Optical Sciences Center. The mirror was cast of Ohara E6 borosilicate glass by the Hextek Corporation.
We will be using aluminum plug-plates to position the optical fibers for the multifiber spectrograph. The plates will be drilled for the predicted temperature of use. However, just before use, the image scale will have to be matched to the fibers. This will be done by translating the primary axially and refocusing the secondary. A 10°C temperature mismatch can be corrected by translations of 2.4 mm and 2.0 mm for the primary and secondary respectively.
The borosilicate glass used in the primary mirror is a low thermal expansion material with an expansion coefficient of 2.8 x 10-6/°C . To prevent thermal distortion of the mirror and mirror seeing from significantly degrading image quality, the temperature of the mirror must be uniform to 0.2°C. (This figure is larger than that established for other telescope using similar mirrors because the resolution of this wide-field optical system is moderate, though adequate to the task.)
Several active temperature control systems have been developed to perform these tasks (Johns and Pilachowski 1990; Siegmund et al. 1990; Lloyd-Hart 1990). We plan to use the rather simple system that is implemented on the ARC 3.5-m mirror. Extensive instrumentation of this mirror and balancing of the ventilation system has demonstrated that the performance of this system will be more than adequate for the 2.5-m telescope optics.
The secondary mirror is supported by three whiffletrees. Each whiffletree is positioned by an axial lead screw driven by a stepper motor via a harmonic drive. This provides control of mirror piston and tilt. The axial step size is 53 nm. This gives a resolution of 7.8 milliarcseconds on the focal plane. The lead screw/bearing assembly is specified to have an accuracy of 250 nm. The performance of these actuators on the 3.5-m telescope secondary has been measured. The differential motion across the diameter of the mirror is 310 nm RMS. This amounts to 57 mas RMS 2-dimensional motion on the sky for the 2.5-m. We expect that much smoother motions, albeit over a smaller range, can be obtained with piezo-electric actuators. These will be mounted in series with the lead screw actuators and used to correct focus during imaging. Similar drives would do nicely to control primary piston and tilt, although it is not yet clear that such high precision will be necessary for that mirror.
The secondary mirror is a borosilicate hot gas fusion blank manufactured by Hextek Corporation. The temperature control requirement to avoid degrading image quality corresponds to a uniformity of 0.2°C. The mass of the secondary is 10% of the primary, and the ventilation flow rate and heat transfer rates are reduced by the same factor. The need to bring cooling fluid to the secondary can be avoided by radiating the excess heat to the sky.
We plan to install in the primary and secondary mirrors a temperature measurement system that we have developed for the 3.5-m telescope to debug mirror temperature control systems. This system uses integrated circuit temperature sensors (Analog Devices AD590) to measure temperatures at one to two hundred locations throughout the mirror. These data are used to adjust flow rates of ventilating air to equalize thermal time constants throughout the mirror. The system, being tested on the 3.5-m mirror, has an accuracy of better than 1°C, a resolution of 5 m°C, and a calibration drift rate of 14 m°C/month RMS.
Temperature changes and, most dramatically, temperature differences between the face and back plate of a mirror, affect its power. This causes a scale change at the telescope focus and contributes to astrometric error, if not corrected in the analysis of the image data. The temperature measurement system described above will monitor changes in the power of the optics and allow the necessary corrections to be made.
A large diameter instrument rotator covers the back of the mirror cell. The spectrographs, camera and fiber plug-plate cartridges will mount to this rotator. Since the spectrographs will corotate with the plug-plates, this eliminates most of the flexing of the fibers that might occur during an integration and should allow for better sky subtraction. Also, as the fibers will be less than 2 meters long, additional benefits include reduction of light loss and materials cost.
The angular accuracy required for the rotator is reduced from that needed for the axes by the ratio of the telescope focal length to the field radius, a factor of 34. This degree of accuracy is quite straightforward to achieve, but is by no means a negligible task. The bearing is a Rotek four-point contact ball bearing. Its high frequency (greater than eight cycles/revolution) lateral runout was measured at about 170 nm RMS per axis at an altitude of 0°. The encoder and friction drive for the rotator are similar to those used for the axes. The drive disk for the rotator is about 2.80 meters in diameter and its high frequency runout is 1.0 µm RMS.
It is necessary, in order to control the image scale of the telescope, to monitor the distance from the focal plane to the vertex of the primary mirror very accurately (25 microns) . The load path connecting these locations is very stiff and we are likely to have excellent control of the temperature of this material as part of the primary mirror temperature control system.
The roll-off enclosure for the telescope is very compact and has a low cross-section for wind loading, both of which reduce the mass and cost of the enclosure base. However, it leaves the telescope completely exposed to the wind and to light sources. These problems are addressed by the wind baffle that closely surrounds the telescope but has a separate low-precision drive system and transfers wind loads to the stationary portion of the telescope building. The wind baffle has a square cross-section that fits closely around the square secondary frame of the telescope.
The sides of the wind baffle, fabricated under contract with CVE Machining, are covered with wind-permeable panels. The panels (H. H. Robertson model 5100), with 25% equivalent open area, consist of interlocking "C" cross-section elements. Light paths through the panel require scattering from a minimum of two surfaces. Thus, with suitable coatings, the panel can be made quite light opaque.
The sky-facing end of the wind baffle contains an annular opening formed by a central disk and a panel with a circular opening (both supported by the wind baffle frame). This opening provides clearance for light from the 3° field of view to reach the telescope entrance pupil. The wind baffle blocks light rays that would otherwise have to be intercepted by the other baffles and prevents direct illumination of the primary mirror by sources more than 27° from the boresight (Figure 2.1).
The inner baffles consist of the secondary baffle (in front of the secondary), the primary baffle (extending through the primary center hole), and the conical baffle (suspended between the primary and secondary). The conical baffle is not usually present in a two mirror telescope design. It is necessary here to avoid unacceptably large central obscuration that would otherwise be the consequence of this wide field optical design. The design shown has a central obscuration of 27%. The conical baffle adds an additional 2%.
We have contracted for an analysis of the baffle design using the Advanced System Analysis Package (ASAP). Preliminary designs have been analyzed using this code and indicate quite satisfactory performance, and we expect that this design will achieve over the whole range of incidence angles greater than about 30° off axis ratios of incident flux to flux in the focal plane (PSNIT) better than 2x 10-6 . This translates, for example, to a scattering contribution to the night sky in the focal plane of about 26.0 mag/arsec 2 by a quarter moon 40 degrees off axis. This is 2% of the dark night sky, and less than half a percent of the moonlit night sky. The ASAP software is being used for the scattered light analysis of many other projects, including the Near IR Camera Multiobject Spectrograph (NICMOS), a second generation Hubble Space Telescope instrument.
The sides of the wind baffle are covered with panels that are 25% porous to the wind. Water tunnel studies indicate that with this porosity, the flow speed around the telescope secondary is reduced to about 1/3 of the free stream flow speed while the flushing time for fluid inside the baffle is still a very rapid 15 to 30 seconds. Water tunnel studies show that flow passing through the channels in the panel diffuses rapidly, i.e., on scales of 0.1 m. No spatially persistent high-velocity jets that might cause wind-induced tracking error are observed.
Centered on the telescope azimuth axis and flush with the telescope enclosure floor and the top of the telescope fork base is a motor-driven circular floor panel that follows the motions of the azimuth axis of the telescope. It supports the wind baffle altitude drive, drives it in azimuth and provides rotating floor space around the telescope for the storage of the camera when a fiber optic cartridge is on the telescope.
Traditional telescope enclosures act as cavity radiators. The net radiation imbalance with a clear sky is roughly 100 watts/m 2 of horizontal projected area. In a well-designed telescope enclosure with low thermal inertia and minimal heat sources, this power (kilowatts for a typical slit size) comes from conduction from the air within the telescope chamber, i.e., via the production of colder than ambient air. This cold air can cause image degradation should it enter the telescope light path.
The wind baffle reduces radiative coupling of the telescope OSS to the sky by minimizing the area of the opening at the end of the telescope. The outer surfaces of the wind baffle are covered with low emissivity aluminum foil tape. Wind baffle surfaces that are well coupled to the sky but which must be black in the visible to absorb scattered light are covered with black chrome tape, a selective emitter with high emissivity in the visible and near IR and low emissivity in the thermal IR. This solution does not work inside the wind baffle since the surface emissivity would have to be nearly zero to reduce the emissivity observed through the opening into a cavity. However, the wind baffle is small enough (unlike a conventional telescope enclosure) that it is practical to circulate fluid through pipes thermally coupled to the wind baffle panels. The temperature of the fluid will be controlled to be the same as the ambient air temperature. Approximately 350 watts of heat will be required.
The control system for each of the two axes of the wind baffle is similar to the control system for the APO 3.5-m telescope enclosure. In this system, a velocity feed-forward signal is obtained from the azimuth axis tachometer. A linear variable differential transformer (LVDT) is mounted so as to produce a signal proportional to the difference in azimuth of the enclosure and telescope. These signals control two dc motors that drive two of the four wheels that support the 100 ton rotating telescope enclosure. Each motor is driven by a separate velocity servo that is closed about a tachometer on the motor shaft. With this system it has been straightforward to control the telescope enclosure orientation to 1 milliradian or better.
The wind baffle reduces wind loading on the telescope OSS by a factor of ten. With care taken in the design of drive and encoding systems, bearings, and the structure, the result should be a telescope with very low wind-induced tracking error that performs at the level necessary to achieve our goals for astrometric accuracy.
Figure 2.7 demonstrates that this level of performance is feasible. These data were obtained on the ARC 3.5m from an intensified CCD camera sampling at intervals of about 13 seconds and integrating for about 1 second while the telescope was tracking open loop. Wind speed was low and the telescope was pointed southeast at an elevation of 60°. These data are uncorrected for seeing effects but are from a 5 minute interval during which the tracking was particularly smooth. The error about a linear drift is better than 100 mas peak-to-peak.
Wind-induced tracking error scales as L 2/3 , where L is a typical scale length (Ulich 1988). Thus, the 2.5-m telescope, which is similar in topology to the 3.5-m telescope, should be about 20% less susceptible to wind-induced tracking error. The use of graphite fiber reinforced epoxy in the secondary truss should result in an additional improvement of similar magnitude.
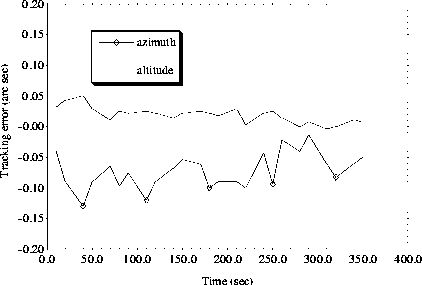
Tracking error in altitude and azimuth for the 3.5-m ARC telescope. The error about a linear drift is better than 100 mas peak-to-peak, and is not much worse about a constant.
During spectroscopic observations, it will be necessary to change plug-plates cartridges about once per hour, and the plug-plate cartridges are expected to have a mass of about 100 kg. For this, and other reasons, the telescope is mounted so that we have access to it via a level track, but still have sufficient ground clearance not to degrade the seeing.

The 2.5-m telescope as installed in October, 1995. Centered on the telescope azimuth axis is a circular floor panel that rotates with the telescope. Access to the telescope is along a horizontal ramp from the support building through the telescope enclosure (at the right edge of the photo) which is in its open position.
Perspective view of the telescope and enclosure with the enclosure rolled off.
The telescope enclosure is a roll-away rectangular frame structure mounted on wheels, and is shown in a perspective drawing in Figure 2.9. During observations, it is rolled downwind from the telescope to the top of the ridge. Large doors on either end of the enclosure are opened during this operation to prevent interference with the telescope and to reduce the wind-load in the direction of motion.
The roll-off approach has several advantages. The thermal ones have been recognized for some time. There are, of course, associated difficulties, particularly wind loading and stray light as discussed above, but for our application the advantages seem compelling enough to compensate for the problems of operating the telescope in the open, to wit:
The design provides several options for handling drive system failures. Power to the building is backed up by an emergency generator. The telescope and wind baffle drive systems allow them to be moved with hand-operated winches into an orientation allowing the enclosure to be closed. The force required to move the enclosure (with the doors open) directly into a 25 m/s (55 mph) wind is 7000 N (1500 lbs). As a back up, this force is supplied by a pair of electric wire rope winches powered by a small general purpose gasoline generator.
Barlow D.J., Blanco D.R., and Poyner A.D., 1987, "Tracking a 150 ton altitude-azimuth telescope to sub-arcsecond accuracy", in Structural Mechanics of Optical Systems II, A.E. Hatheway, ed., SPIE 748, 17.
Bowen I.S., and Vaughan A.H., 1973, Applied Optics, 12, 1430.
Davison W., and Ulich B.L., 1982, "Performance of the Multiple Mirror Telescope (MMT): II. Mechanical Properties of the MMT", in International Conference on Advanced Technology Optical Telescopes, G. Burbidge and L.D. Barr, Ed., SPIE 332, 9.
Gunnels, S.M., 1990a, "Detail design problems and their solutions: Apache Point Observatory 3.5-m telescope", in Advanced Technology Optical Telescopes IV, L.D. Barr, Ed., SPIE 1236, 854.
Gunnels, S.M., 1990b, "Direct Friction Drives", Magellan Project Report No. 18.
Johns, M. W., and Pilachowski, C., 1990, "WIYN 3.5-m telescope project", in Advanced Technology Optical Telescopes IV, Barr L.D., Ed., SPIE, 1236, 2.
Johns, M. W., 1991, "Azimuth Bearing Study for the WIYN 3.5 Meter Telescope", Wisconsin, Indiana, Yale, NOAO 3.5 Meter Telescope Internal Report, 1991, WODC 02-06-01.
Lloyd-Hart, M., 1990, "System for precise temperature sensing and thermal control of borosilicate honeycomb mirrors during polishing and testing", in Advanced Technology Optical Telescopes IV, L.D. Barr, Ed., SPIE 1236, 844.
Mannery E.J., Siegmund W.A., Balick B., and Gunnels S., 1986, "Design of the Apache Point Observatory 3.5 m Telescope IV. Optics Support and Azimuth Structures", in Advanced Technology Optical Telescopes III, L.D. Barr, Ed., SPIE 628, 397.
Mannery E.J., Siegmund W.A., Balick B., and Gunnels S., 1986, "Design of the Apache Point Observatory 3.5 m Telescope IV. Primary Mirror Support System", in Advanced Technology Optical Telescopes III, L.D. Barr, Ed., SPIE 628, 390.
Poyner A.D., Montgomery J.W., and Ulich B.L., 1986, "MMT Pointing and Tracking", in Advanced Technology Optical Telescopes III, L.D. Barr, Ed., SPIE 628, 9.
Schier J.A., 1990, "Torque Perturbations in the Magellan Main Drive Motors", Magellan Project Report No. 16.
Siegmund, W.A., Stepp, L.M. and Lauroesch, J., 1990, "Temperature Control of Large Honeycomb Mirrors", in Advanced Technology Optical Telescopes IV, L.D. Barr, Ed., SPIE 1236, 834.
Ulich B.L., 1988, "Overview of Acquisition, Tracking, and Pointing System Technologies", in Acquisition, Tracking, and Pointing II, SPIE 887, 22.