Thermalization and Production of Neutrinos in Dense Nuclear Matter

Thermalization: Supernova theorists have long recognized the importance of neutrino-electron scattering as an energy exchange mechanism in supernovae. Much effort has been exerted to include the full collision integral in the solution to the neutrino Boltzmann equation. Neutrino-nucleon scattering has been included in simulations as well, but never as an energy exchange mechanism. It has always been included as an important source of opacity, but the energy exchange has been assumed negligible. In fact, although the average energy transfer per scattering is relatively small in these interactions, the cross section for scattering is much larger than that for neutrino-electron scattering. It seems plausible, then, that each process may play an important role in supernovae -- each with a different regime of importance as an energy exchange mechanism. To test this, we have developed an algorithm for solving the full collision term of the neutrino Boltzmann equation in an isotropic homogeneous thermal bath of scatterers. We set the temperature, density, and composition of the bath to reflect representative points at snapshots in time within a core-collapse supernova. To the right we include a movie showing equilibration via both scattering processes and a figure, which summarizes the thermalization rate.

Movie

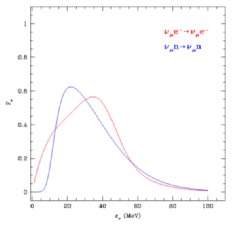
Rates

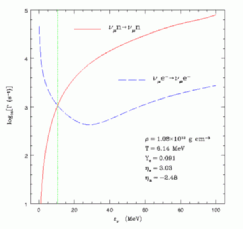
Production: Nucleon-nucleon bremsstrahlung has recently been recognized as an important neutrino production mechanism in supernovae. Other neutrino production processes include the charged-current reactions, which produce electron and anti-electron neutrinos, plasmon decay, and electron-positron annihilation. The latter two processes, like bremsstrahlung, produce neutrinos of all species. Bremsstrahlung has been ignored as a production mechanism in fully dynamical supernova calculations to date as it has been assumed sub-dominant in comparison with electron/positron annihilation. In order to test the validity of this approximation, we study production of mu and tau neutrinos in a isotropic thermal bath. Given zero initial phase-space occupancy at all energies, we solve the Boltzmann equation for the time evolution of the neutrino phase-space distribution function using the full production integral. We follow both neutrinos and anti-neutrinos. The final equilibrium phase-space distribution should be Fermi-Dirac with zero chemical potential. 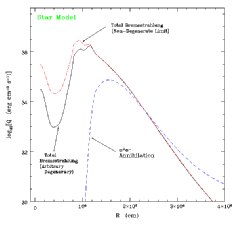To the right we include a movie showing production of the equilibrium Fermi sea of neutrinos via both bremsstrahlung and electron/positron annihilation. We also include a figure summarizing the relevant rates at two different points in a representative stellar profile.

Movie

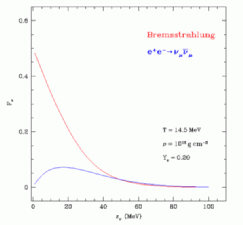
Rates

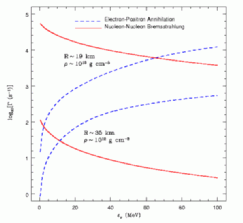
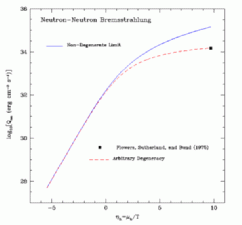
Nucleon-Nucleon Bremsstrahlung: In conducting the production study above, we employed the one-pion exchange approximation and made some simplifying assumptions concerning the resulting matrix element. We calculated the Boltzmann equation production term and the spectrum in the non-degenerate limit and at arbitrary degeneracy. Note that we include the contributions from neutron-neutron, proton-proton, and neutron-proton bremsstrahlung in computing the final rates. To the right are two figures that illustrate the difference between the non-degenerate limit, which generally over-predicts the rate, and the case of arbitrary degeneracy.