Here is an activity which ties together both distance measurement and the expanding universe. It uses the spectrum of the supernovae, which are exploding old stars, to determine the rate of the expansion of the universe and the brightness of the supernovae as standard candles to determine distance. Like the galaxies whose "wattage" could be determine just by looking at them, supernovae type can be determined by looking at their spectrum, which is explained in the red shift section. A certain type of supernovae, type Ia, has a spectrum which shows that lots of hydrogen is present near the explosion. Astronomers have determined that this type of supernova has a maximum brightness. This maximum is calculated by using physics and the mass of the dying star. Although recent discoveries have shown that this maximum is not always the exact same number, it is a good approximation to use that all supernovae type Ia have a maximum absolute brightness of -19 magnitudes. This is the measurement of the brightness of the supernova as if you were 10 parsecs from it, measured according to an ancient system developed by Hipparcos.

In this system, Hipparcos divided up all the stars he could see into six categories, 1-6. He labeled the brightest stars "1" and the dimmest ones "6". However, he labeled these stars as he saw them (which is now called the apparent brightness), not as if he were 10 parsecs from them (which is now called absolute brightness). As we discussed in the Galactic Brightness Section, this difference in brightness is important because brightness falls off with distance according to the inverse square law

.

Supernovae are so intrinsically bright that their magnitude ratings go all the way to an absolute magnitude of -19. This means a supernova which is 10 parsecs away would be 1.5*10⁷ times brighter than Sirius, the brightest star in the nighttime sky.

To find out why look here.

Since we now know how bright the supernova can possibly get, we can calculate the distance to it by making observations of how bright we perceive it, which is called the apparent brightness, and then using the formula:

.

In this formula,

In order to measure the maximum apparent brightness, astronomers must first discover a supernova, which is relatively easy because supernovae are so bright. A supernova which exploded in 1054 A.D. according to the accounts of an imperial astronomer from the Sung Dynasty, was visible even during the daytime and can be seen today in the crab nebula:

The Crab Nebula ²³

All the astronomers must do is observe many galaxies and watch for any bright patches to appear as seen in this picture:

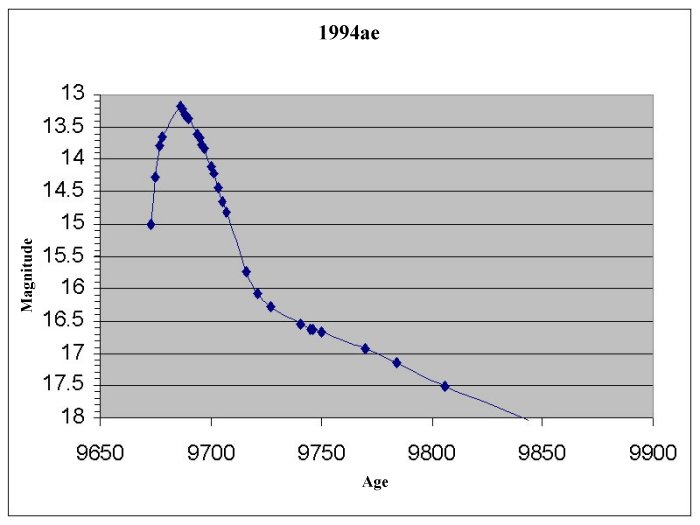
Supernova 1987A ²⁴

Then they must take the spectrum of the supernova to confirm that it has the right "finger print", or spectrum to be a supernova. If astronomers wish to use the supernova for a distance measurement they then must observe the spectrum as often as they can for several days, preferably every day. They can then make a plot like this one:

The x axis is in units of days, but it is labelled according to a shortened form of Julian Dating. In this system, astronomers decided to start counting days on January 1, 4713 BC (Day 0) and then added one day for every day after that. This number is then shortened by subtracting 2440000, leaving the number around 9000 for dates near 1990 A.D. The y axis is in units of the observed brightness in magnitudes; remember, brighter supernova have lower magnitudes. The line connecting data points is drawn in for convenience and is merely a best fit line intended to give some idea of the usual shape for these sort of curves. As you can see from the graph, supernovae grow brighter until they reach a maximum brightness and then grow fainter. In absolute magnitudes, this brightness is about -19, however you will notice that they appear much dimmer because the supernovae are so far away.

Back | Next