
The most crucial requirement for astrometry is the need to drill holes accurately for the spectroscopy. The camera and telescope will be made much more accurately and stably than are required for this, however, and we hope that the survey will, when finally calibrated, yield very good positions. The galaxy positions for any given spectroscopic plate will ultimately come from 4 to 6 independent imaging strips that needed to be joined together with high accuracy. This pretty much requires that the galaxy positions from each strip be calibrated absolutely on the sky.
The maximum allowable de-centering error is determined by the requirement that the amount of light falling on a fiber not be seriously decreased for a worst-case galaxy or QSO. The amount of light that a fiber sees is a function of the total magnitude of an object, its concentration factor, the seeing, clouds, and fiber de-centering. Kent (1985) has measured the light concentration factors for a large number of galaxies of all types on this system. Based on this information, we have simulated observations of galaxies with properties spanning those of typical galaxies including the effects of seeing and fiber de-centering; the results are shown in Figure 6.1. As might be expected, point sources suffer more from de-centering errors than fuzzy extended objects, but the absolute amount of light that is collected is still higher for point sources until the de-centering error becomes quite sizable. Therefore, if exposure times are governed by the amount of light that comes from the low surface brightness galaxies, we can tolerate de-centering errors of order 1" . For the QSO spectroscopy, the tolerances are tighter (all QSOs being point sources) since we are trying to observe to a limit 1 mag fainter than that for the galaxies. Somewhat arbitrarily, we set the criterion for the maximum tolerable pointing error to be that it does not cause us to lose more than 20% of the light - this translates to a maximum error in radius of 0.75" . If the distribution function of errors is uniform over a circle of radius 0.75" , then the rms error in radius is 530 milliarcsec (mas) and the error in either the x or y coordinate is 375 mas.
The total de-centering error is the sum of contributions from astrometry, plate drilling, focal plane transformation, differential refraction, collimation, and guiding during observations. The collimation errors arise from the fact that the plate and glass correctors rotate relative to the primary and secondary mirrors, which introduces a rotating distortion pattern if the telescope optics are not perfectly collimated. In order that astrometric errors not dominate the error budget, we demand that the rms astrometric error be less than half the total allowed. Hence we require that the astrometry have errors of no worse than 187 mas in any coordinate, or 265 mas in radius. Table 6.1 gives our estimates of the allowed contributions from all sources. The differential refraction error is a worst-case situation for observing extreme southern or northern fields at high air mass.
| Source | RMS (milliarcsec) in Radius |
|---|---|
| Drilling | 270 |
| Astrometry | 265 |
| Differential Refraction | 260 |
| Collimation | 170 |
| Guiding | 40 |
| Focal plane mapping | 20 |
| Combined | 490 |

The effect of decentering. The apparent magnitude of light passing through a 3" diameter fiber as a function of de-centering offset is shown. In each panel, the different curves correspond to galaxies with differing light concentration factors, ranging from point sources (top curve) to values typical of Sd galaxies (bottom curve). All galaxies are assumed to be viewed face-on. The top and bottom panels are for 1" and 2" seeing respectively. All galaxies have a total apparent magnitude of 18.
There are several possible approaches to the problem; one might, for example, scan a field with a high density of astrometric standards (such as the fields established for calibrating the instruments -- see the next section) enough times a night to determine the scale on each chip, its orientation, and its location with respect to some fiducial point in the array. Another approach, and the one we favor, is to use astrometric standards we encounter in the course of the imaging to update continuously a coordinate system constructed from a large number of fainter stars whose celestial coordinates we do not know. To do this, it is necessary to increase the dynamic range of the imaging array quite substantially and at the same time provide some way to determine the separations of the six CCD columns.
We will accomplish both of these objectives by the use of an augmentation to the imaging array which consists of 22 2048 x 400 astrometric CCDs, as illustrated in Figure 2.2 and discussed from the point of view of mechanics and electronics in Chapter 4 and data handling in Chapter 10. These chips have a shorter effective exposure time than do the photometric chips because they have fewer rows. In addition, we will use a neutral filter with a density of about 1.2 (3.0 magnitudes) in front of these chips. These two effects, plus differences in quantum efficiency between the two types of chip, will allow us to reach an r' magnitude of 8.5 before saturation. The high density astrometric catalog that we will use goes substantially fainter than this bright limit. We will be able to do quite accurate astrometry with this sensitivity down to about r'=17.0 , an overlap with the imaging array of 3m.0 , in which range there are more than 300 stars (hereinafter referred to as the `overlap stars') per square degree everywhere in the survey region. We encounter at least 2 overlap stars per second, and at any given time there are about 3 such stars on a given astrometric chip and 15 on a given imaging chip. The five astrometric sensors across the top (in the first row) overlap the six sensors in the second row (and thus the photometric CCD columns) by an arcminute on each end and serve to tie the columns together. A star suitable for this purpose is encountered in each of these ten overlap regions about every 50 seconds.
For arrays 400 pixels high, the integration time for the astrometric sensors is about 11 seconds. As was discussed in Chapter 4, we would like to use sensors which are taller, in order to get more integration time and thus better average the seeing wander, but both geometric and financial constraints limit us to these chips.
The best choice for an astrometric catalog for the primary standard stars is clearly the Tycho catalog, due to be released in May, 1997. This catalog has a high density (about 106 stars total over the celestial sphere, an average density of 25 stars per square degree with 10 stars per square degree at the North Galactic Pole) and high astrometric accuracy (estimated to be .030" in each coordinate) (Høg et al., 1992).
The only shortcoming of the Tycho catalog is its lack of accurate proper motions. However, partly in anticipation of this problem, the U.S. Naval Observatory (USNO) has prepared an astrometric catalog based upon plates taken with their 8-inch Twin Astrograph (the mean epoch of the catalog is about 1981). This Twin Astrograph Catalog (TAC) contains virtually all of the Tycho catalog stars and has, on average, over 20 stars per square degree to a magnitude of about V=12 . The stellar density at the North Galactic Pole is about 10 stars per square degree. TAC is supplemented by accurate proper motion determinations based upon a new solution of the old Astrographic Catalog (AC) Zone plates. TAC will be accurate (in each coordinate) to about 0.080" at epoch, with an uncertainty in the proper motion of about .003"/ year yielding positional accuracies of 0.10" at J2000. USNO assigned top priority to reducing those zones contained within the SDSS survey area and those reductions are now complete. As soon as Tycho is released USNO will provide SDSS with proper motions for the catalog stars. The resulting positions should be accurate to about .040" per coordinate at the epoch of SDSS observations.
Calibration of the astrometric array is done in two separate processes. The first process is to determine the positions of the individual CCDs relative to one another as they are mounted on the rigid camera base. This will be done by scanning the telescope through a portion of sky with a dense grid of stars with very accurate astrometry. The USNO has prepared several such astrometric calibration fields using observations obtained especially for this purpose with the 8-inch Transit Telescope at Flagstaff. Sixteen fields, each 3.2 degrees in width and 1/2 hour (7.5 degrees) in length, have been established all around the equator. The limiting magnitude is typically 17.1, stellar densities vary from a few hundred to a few thousand per square degree (depending upon Galactic coordinates) and one-dimensional internal positional errors for stars brighter than about 15.m5 are < 0.025" , falling to .050" at 17.m0 . Comparison with preliminary Tycho data indicates that the (external) astrometric accuracies are better than .050" .
The second process is to determine the actual scanning path through the sky during a particular drift scan and the orientation of the array relative to that path. For the discussion which follows, consider the calibration of the array of CCDs as a single large CCD.
The telescope nominally tracks a great circle. Introduce (µ, nu ) as great circle coordinates. The longitude µ increases along the great circle and the latitude nu increases perpendicular to the great circle; we have nu =0 along the great circle itself. For the moment we ignore the complications of precession, refraction, etc.
The CCD device has coordinates (X,Y) . The units are device pixels. X increases perpendicular to the scan direction (to the North). Y increases along the scan direction (to the East).
The CCD image has coordinates (x,y) . The units in the x direction are ordinary device pixels (also called x -pixels below when it is necessary to distinguish the two); the units in the y direction are y -pixels. x increases perpendicular to the scan direction (to the North). y increases along the scan direction (to the East). The distinction between device and image coordinates is necessary for drift scan images because the two do not necessarily coincide exactly. For example, the y axis is always aligned precisely with the drift direction of the telescope even if the Y axis is rotated slightly with respect the the drift direction. Also, a y pixel may not necessarily map to the same number of arcseconds as an x pixel; it will do so only if the CCD clocking rate perfectly matches the drift rate of a star across the CCD.
Introduce the following parameters:
If the telescope tracking and rotator alignment are not perfect, we have two extra parameters to describe the misalignments:
To good accuracy, we have

Next, we consider the complications introduced by the fact that we have a mosaic of CCDs. Select one CCD as a reference. Then each other CCD has positional offsets Dx , Dy in mm relative to the first and a rotation thetab with respect to the coordinates defined by the reference CCD. (We shall also add an extra parameter to allow for a difference in scale factor). For N CCDs in the array, we need to calibrate N-1 times 3 (or 4) parameters. To do so we will scan across the high density astrometric standard fields.
In addition to the information provided by scanning the astrometric standards, we get additional information from multiple crossings of the front and rear CCDs in the array by the same overlap stars. This provides us with a near-continuous monitoring of two numbers: the front-back x differential and the front-back y differential. If we have a priori calibrations of Dx, Dy, and f for the front and back CCDs, then we reduce the original six free parameters in Eq. (6.1) to essentially four (the angle thetab adds another parameter, but it can be determined from the front-back crossings quite accurately). The usefulness of the extra 2 measurements will depend on being able to measure Dx and Dy accurately and on the time behavior of the calibration parameters. It may be possible to use the r' (and even the g' if we are careful about differential refraction) photometric CCD to add additional crossing measurements (this requires that the photometric CCDs be mounted with the same rigidity and thermal behavior as the astrometrics).
Next, we consider the time dependence of the parameters. We require that parameters be stable on a time scale long enough that we can scan over enough standard stars to get a satisfactory calibration. We use the lowest density of astrometric reference stars (10 per square degree, found at the North Galactic Pole) in what follows. The camera images a swath which is 2.3 degrees wide and if we scan at a sidereal rate we will cover 2.3 square degrees every 4 minutes. Hence, we will be scanning over at least 6 Tycho stars per minute, each star yielding 2 measurements ( x and y ). In 10 minutes we thus have 60 pairs of measurements to constrain 6 parameters. Therefore we have some freedom to introduce a small number of extra degrees of freedom per parameter for each 10 minutes of integration in a scan, and our error estimates later will make this assumption.
Finally, we consider the rotations and distortions introduced by such effects as precession, nutation, and aberration. There are seven effects to worry about. Precession, nutation, polar motion, and UT1-UTC offsets correspond to rotations of the sky without distortion. These will be accounted for already by the telescope tracking algorithms; any residual corrections will be absorbed in the 6 constants of the calibration process. Aberration and refraction correspond to a distortion of the (x,y) system relative to the (µ, nu) system, and refraction is large enough that second order corrections will be needed. They can likely be calculated accurately enough that there is no need to introduce additional unknown parameters. Low order imperfections in the telescope drive surfaces will be removed by the telescope control computer. High order imperfections will appear as time variations in the tracking sensitive parameters.
It is appropriate to describe here the tracking algorithm to be used by the telescope. The telescope control computer keeps track of a specific point in the telescope focal plane that is called the boresight. The boresight is not fixed in the array but is at one of two places for the two strips that compose a stripe (see Figure 2.2). It is the boresight that will track great circles. Technically, the boresight tracks a path that is a great circle in J2000 coordinates as viewed from the solar system barycenter. Aberration and refraction distort the path so that it is no longer a great circle as viewed from the ground; however, the distortion is small enough that it does not introduce any significant curvature in the paths of stars in the drift scans. The Y axis of the array is oriented along the apparent equator of the great circle as viewed from the ground. Refraction and aberration also distort the scale of the great circle such that a step of 1 arcsec in J2000 coordinates does not correspond to 1 arcsec as viewed from the ground. The tracking rate of the telescope (which is computed using J2000 coordinates) will be adjusted so that the apparent rate of stars drifting across the focal plane is strictly constant.
Once the positions of the overlap stars are calibrated, one can imagine transferring the coordinate system so established to the photometric array in any one of a large number of ways, the most straightforward of which is simply to use the overlap stars as secondary astrometric standards. The photometric CCDs will certainly wander with respect to the astrometric array in response to thermal and flexural changes, but on a timescale which is very long compared to that required to tie to the astrometric system with very high accuracy. In particular, the output of the r' chips can be treated very much as the output of the astrometric chips is treated, and provides an interpolative point between the leading and trailing chips to monitor drive irregularities in both coordinates at frequencies corresponding to the residence time of a star on the array. These frequencies will be very high compared to any relative drifts between the astrometric and photometric arrays.
Will we be able to achieve the desired accuracy of 260 mas rms per coordinate? Here we look at all the possible error sources.
Table 6.2 gives a summary of all errors, statistical and systematic, in calibrating the secondary standard stars; such a set would then be used to calibrate a single frame from the photometric array. The following assumptions go into the table:
| Source | RMS Radius Error (mas) |
|---|---|
| Error in primary standards | 24 |
| Seeing in primary standards | 25 |
| Seeing in secondary standards | 42 |
| Shot noise in secondary standards | 20 |
| Uncorrected tracking errors | 55 |
| Combined | 80 |
Here we discuss the errors individually.
We assume that the Tycho positions have (conservatively) an rms error of 50 mas per coordinate at epoch J2000 and that we encounter a minimum of 6 catalog stars per minute. The error quoted is for a single scan of the telescope; repeated scanning, obviously, will not reduce this contribution.
There is some discussion of seeing at APO in Chapter 3.5; here we concentrate upon theoretical aspects.
The evaluation of the contribution which seeing makes to the position error for a telescope in TDI mode is similar to the considerations used for ordinary imaging. Under the assumptions that (1) the seeing is described by Kolmogorov turbulence with some outer scale rmax and whose amplitude is characterized by a Fried parameter r0 with which the long-integration-time seeing FWHM w scales inversely ( w ~ lambda /r0), (2) the outer scale is larger than the telescope aperture, and (3) the integration time is longer than the time it takes the outer scale in the seeing screen to traverse it can be shown that, at a given wavelength, (see, e.g., the developments in Roddier, 1981)
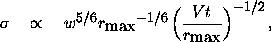
where sigma is the one-dimensional standard deviation in the position, t is the integration time, and V is the characteristic wind velocity at the height where the seeing originates. With these assumptions the error is independent of the telescope aperture. There is not much data on the size of the outer scale, and it is probably variable, but it is usually assumed to be of the order of 10 meters.
We have analyzed a data set obtained with the four-shooter camera on the Hale telescope at Palomar by opening the shutter for a long period with the telescope parked with the instrument aligned so that the trajectories of stars are accurately along the CCD columns. The wander in those trails is entirely the consequence of seeing, and the behavior of the autocovariance function of that wander gives one amplitudes and time dependence. It appears from this data set that the characteristic time associated with the outer scale, rmax/V , is about 0.5 seconds; this is determined by the integration time at which one enters the t-1/2 behavior above. For a wind speed of 20 m s -1 , which is reasonable, the outer scale is about 10 meters. The seeing at the time the trails were taken was 2.0 arcsec FWHM, and the image wander averaged over 11 seconds was 56 mas. Scaling to 1.0 arcsec seeing, we would expect about 32 mas. We have also analyzed driftscan data from the Mt. Hopkins 1.2 meter telescope. TDI mode driftscans of the same portion of sky were obtained in two separate years; the instrument was a Ford Aerospace 2048 CCD with 0.66" pixels and an integration time of 50 seconds; the seeing was about 1.5 arcsec. Bright stars in the two scans were matched up and positions compared. A plot of the right ascension residuals (after removing an offset and drift) is shown in Figure 6.2. The data span about 40 minutes. The rms difference between the two sets is 120 mas, or 85 mas per single observation, or 60 mas for 1" seeing. The residuals show considerable correlation over time scales of order a few minutes with an amplitude rather larger than seeing theory predicts. All told then, we can expect seeing errors to be no better than 32 mas, but no worse than 60 mas.
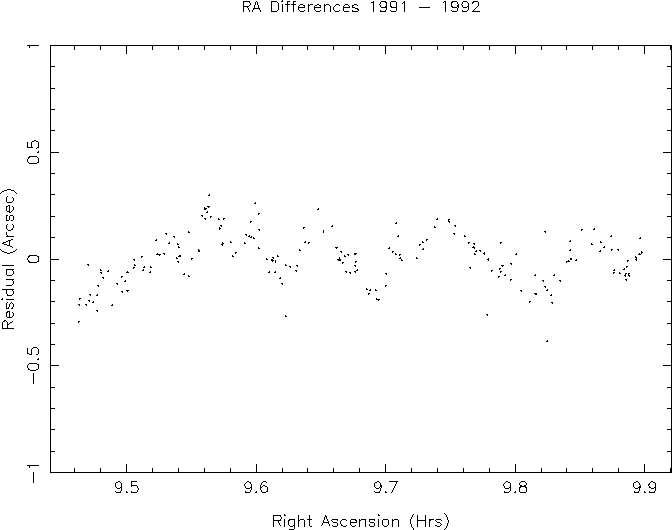
Comparison of star positions from drift scan data taken in separate years. Only the residuals in right ascension are shown (the declination residuals have a similar behavior). An offset and slope have been removed from the data. The rms difference is 0.12" . The data span about 30m of time. For both sets of data, the telescope was stopped and the drift scanning was done at sidereal rate.
Shot noise can be a significant source of error for the measurement of the position of an individual faint star (it is almost entirely negligible -- on the order of a couple of mas -- for bright stars with many thousands of electrons in the image). Computer simulations have been carried out to estimate the size of this effect using realistic values for dark current, read noise, quantum efficiency and sky background for the astrometric chips. At r' = 17.0 , the faint end of the `overlap' star range and, hence the worst (though most frequent) case, simulations show that the astrometric error contribution from shot noise is about 50 mas per coordinate per star at this level. The shot noise contribution to the astrometric error for a frame depends upon the number of such stars on the frame. No fewer than 10 such stars should show up per frame, and not all will be at the faint limit. The adopted value, 20 mas in radius, should be conservative enough.
Chapter 2 has reviewed the expected tracking performance of the telescope. We note that the calibration procedure automatically absorbs any constant offsets and linear drifts in the tracking, so only deviations with respect to a linear drift in the tracking are of concern. The error estimates given here are based on acceptance test measurements of the assembled 2.5-M telescope major components at Apache Point at the maximum tracking rates we expect to encounter.
We have shown that we can achieve astrometric accuracy which is plenty good enough to place the fibers. But how well might we be able to do in a finally calibrated version of our catalog? We have a couple of schemes in mind to improve the telescope tracking performance and if we implement them successfully we should become seeing-limited.
Table 6.2 assumes a rather simplistic approach to the determination of the transformation parameters, in which the fact that one has very many more secondary standards which determine some of the parameters to very high accuracy is not used to advantage. In particular, the large contribution from seeing in the secondary standards can likely be reduced to levels below that for the primaries if one is careful; in any case, the error is seriously overestimated because of the assumption of perfect correlation among the secondaries.
Thus the astrometric errors can probably be brought down to of the order of 50 mas in radius, or 35 mas in each coordinate. This accuracy would be of enormous utility for statistical parallaxes, tying radio source maps to their optical counterparts, and the eventual measuring of proper motions for the many faint main sequence stars the survey will find. If we do this well, repeating the northern survey to measure proper motions and long-term variability becomes an exciting possibility.
Kent, S.M., ApJSuppl 59, 115, 1985.
Høg, E., Bastian, U., Hansen, P.C., van Leeuwen, F., Lindegren, L, Pedersen, H., Saust, A.B., Schwekendiek, P., and Wagner, K., AstrAp 258, 201, 1992.
Roddier, F., Progress in Optics XIX, 281, 1981.