Writeup 3: Planetary Thermodynamics
Consider a planet of radius ![]() a distance d from a star of radius
a distance d from a star of radius
![]() . The planet receives a certain amount of energy from the
star, which it reradiates as a blackbody. Our aim is to use this
information to calculate the equilibrium temperature of the planet.
Let's start with figuring
out how much energy per unit time it receives. The planet has a
cross-sectional area of
. The planet receives a certain amount of energy from the
star, which it reradiates as a blackbody. Our aim is to use this
information to calculate the equilibrium temperature of the planet.
Let's start with figuring
out how much energy per unit time it receives. The planet has a
cross-sectional area of ![]() (do you understand why we don't
write
(do you understand why we don't
write ![]() ?), so the fraction of all the energy the star
puts out that the planet receives is that cross-sectional area,
divided by the surace area of the sphere out to the planet:
?), so the fraction of all the energy the star
puts out that the planet receives is that cross-sectional area,
divided by the surace area of the sphere out to the planet:
![]()
Thus the energy per unit time received by the planet is the luminosity
of the star, times that ratio. The star radiates like a blackbody, so
its luminosity is ![]() . Thus
the total amount of energy per unit time received by the planet is:
. Thus
the total amount of energy per unit time received by the planet is:
![]()
The above is correct if the planet absorbs all the energy
incident upon it. Does it really do so? No, some of the energy is
reflected. We refer to the albedo A as the fraction of energy
per unit time incident upon on the planet that is reflected; 1-A is
the amount absorbed. So with this factor included, the total amount
of energy per unit time absorbed by the planet is:
![]()
Now, all that energy has to go somewhere. Where does it go? It is
radiated by the planet in the form of blackbody radiation. If the
planet has temperature ![]() , the amount of energy it is putting out per
unit time is just
, the amount of energy it is putting out per
unit time is just
![]()
We're almost done. If the planet is in equilibrium, the amount of
energy it is absorbing has to equal the amount it is emitting. So we
can equate these last two expressions:
![]()
What a mess! But lots of things cancel. In particular, note
that the radius of the planet itself ![]() cancels, as does
cancels, as does ![]() . We're left with:
. We're left with:
![]()
Let's take the fourth root of both sides to get our final result:
![]()
Pretty cool, eh? The equilibrium temperature of a planet is
determined by the size, temperature, and distance to its parent star,
but not on its own size.
Let's plug in numbers for the Earth. Here ![]() K, the
albedo is about 40%,
K, the
albedo is about 40%, ![]() km, and
km, and ![]() . Thus:
. Thus:
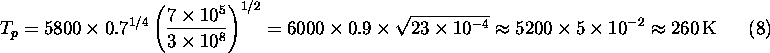
This is below the freezing point of water; if this was really the true mean temperature of the Earth, the oceans would be largely frozen. What are we missing? There is another effect, which we will discuss in detail soon, namely the trapping of heat radiation from the Earth's surface, known as the greenhouse effect, which raises the mean temperature at the Earth's surface to a comfortable 300 K.
What does it mean to say that a gas has a certain temperature? The
hotter something is, the more kinetic energy each of the
particles making up the gas has. Indeed, in thermal equilibrium, all
particles have the same kinetic energy:
![]()
where k is Boltzmann's constant which we saw in writeup 2. The
kinetic energy of a particle of mass m with speed v is ![]() . Thus in a gas of particles of different masses, the
lower-mass objects are moving the fastest.
. Thus in a gas of particles of different masses, the
lower-mass objects are moving the fastest.
Now consider a planetary atmosphere, say that of the Earth. The typical speeds of molecules at room temperature can be approaching a kilometer per second (calculate it yourself). Ask yourself, if the molecules are moving around so enormously fast, then why aren't we blown down by tornado-force winds all the time? There is a maximum speed that a molecule can move in the atmosphere, before it reaches escape velocity. Let's now think about what this means.
Throw a ball upwards. It gains gravitational potential energy, and
loses kinetic energy, until it comes (momentarily) to a standstill,
and falls back down. ``What goes up must come down'', but that's not
the full story. If you throw it up hard enough, it can have more
kinetic energy than potential energy, and escape from the Earth
altogether. Otherwise, we would never be able to lunch spacecraft to
visit other planets. Let's calculate. The gravitational potential
energy of an object of mass m at the surface of a planet of radius
R and mass M is:
![]()
(It is negative; as you go upwards, your potential energy
increases).
If the total energy, gravitational plus kinetic, of an object is
positive, it will escape. Thus the condition for escape is:
![]()
Solving for v, and recognizing that m drops out, gives:
![]()
Plugging in these numbers for the Earth gives 7 kilometers per second. Thus any object travelling upwards at more than 7 kilometers per second will escape the Earth's gravity, be it a rocket, or a gas molecule.
If we calculate the thermal speed of a hydrogen molecule (H2) at room temperature, we find 2 km/s, seemingly comfortably below the escape speed of the Earth. But the Earth's atmosphere has essentially no hydrogen molecules in it at all, even though, as we've seen, hydrogen is the most abundant element in the universe. What gives? The answer is that it is not true that all the molecules at a gas have a kinetic energy given by 3/2 kT; that is just an average number. Indeed, there is a broad distribution of speeds (following a mathematical form originally given by James Clark Maxwell), and there remains an appreciable fraction of molecules travelling at speeds several times that of the average. These molecules will escape. Collisions between the remaining molecules will bounce some of them up to these high speeds, and these will subsequently escape as well, and so on. Over a period of time, the hydrogen in our atmosphere will gradually leak out. These notions will be very useful to us when we consider the difference between the atmospheres of the Earth and Jupiter.
Michael Strauss