Two Interacting Blastwaves |
Woodward, P. and Colella, P., "The Numerical Simulation of Two-Dimensional Fluid Flow with Strong Shocks", J. Computational Physics, 54, 115-173 (1984). The problem is shown in Sections IV and VI and results in Figures 2h and 6(a-g).
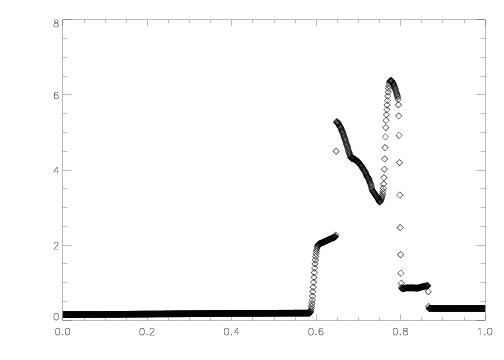
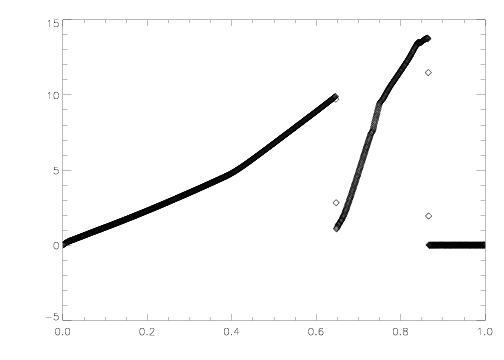
This test is a very simple hydrodynamic shocktube filled with a γ=1.4 gas of uniform density ρ = 1 and three different pressures. In the leftmost tenth the pressure is 1000, in the rightmost tenth the pressure is 100, and in the center the pressure is a much smaller 0.01. The boundary conditions are reflecting at both ends. Immediately both sides launch strong shocks towards the center and strong rarefactions towards the walls. The various initial shocks, rarefactions, and their reflections proceed to interact nonlinearly.
This test is very difficult to solve on an Eulerian grid due to the strong shocks and multiple interactions with rarefactions and contact discontinuities. At high resolution (more than 1000 zones), we find the Roe solver fails at one interface for one instant late in the evolution -- the algorithm in Athena automatically applies the HLLE solver for that one interface and that one cycle.
Results computed with Athena using the third-order Roe solver on an array of 1200 cells with a Courant number of 0.8 and γ = 1.4. The density and velocity are plotted at time 0.038. These plots can be compared to Figure 2(h) in the reference. The contact discontinuitie at x=0.6 is not as sharp as it is with a Lagrange-plus-remap version of PPM (PPMLR). This seems to be a generic trait of direct Eulerian versus Lagrange-plus-remap codes.
 |
 |