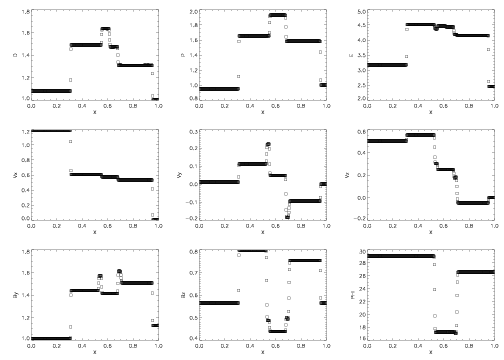
Ryu and Jones Test 2A

Reference:

Ryu, D. & Jones, T.W., "Numerical Magnetohydrodynamics in Astrophysics: Algorithm and Tests for One-Dimensional Flow", Astro. J., 442, 228-258 (1995). The test is described in Section 4.

Description:

This test is an MHD shocktube, where the right and left states are initialized to different values. It involves a three-dimensional field and velocity structure and rotation of the plane of the magnetic field. The left state is initialized as (ρ, v_x, v_y, v_z, B_y, B_z, E) = [1.08, 1.2, 0.01, 0.5, 3.6/(4π)^1/2,2/(4π)^1/2,0.95] and the right state [1,0,0,0,4/(4π)^1/2,2/(4π)^1/2,1]. The background magnetic field is 2/(4π)^1/2.

What's important about this test?

This test contains fast shocks, slow shocks, and rotational discontinuities which propagate to each side of the contact discontinuity. The ability of the scheme to capture all 7 waves in MHD can be checked with this single test.

Results in one-dimension:

Results computed with Athena using the third-order Roe solver with 512 cells with a Courant number of 0.8 and γ = 5/3. The plot shows the solution at a final time of 0.2. The plot shows from left to right: a fast shock, a rotational discontinuity, a slow shock, a contact discontinuity, a slow shock, a rotational discontinuity, and a fast shock. The rotation of the magnetic field is given by ψ = tan^-1(B_z/B_y). These results can be compared to Fig. 2a in RJ.

Results in three-dimensions:

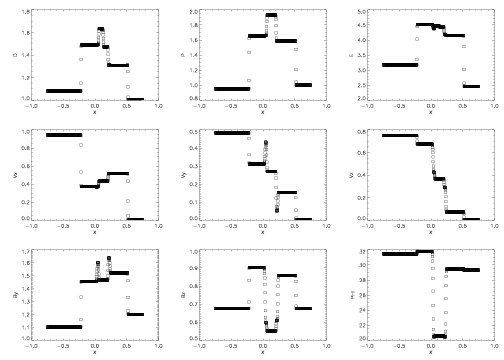
Results computed with Athena using the second-order Roe solver on a domain of size 1.5 X 1/64 X 1/64 with a grid of 768 X 8 X 8 cells with the initial discontinuity rotated to the grid. The description of the geometry of the initial conditions is complicated, see the 3D Method paper for details. The effective resolution perpendicular to the discontinuity is 512 grid cells, identical to the 1D case. Special periodic boundary conditions are used in the y- and z-directions to map the solution in a direction parallel to the interface (perpendicular to the direction of propagation of the waves) -- this direction is not parallel to the grid lines. The solution is shown at a final time of 0.2. There is excellent agreement between all of the structures in the solution in 3D with the 1D plot above -- there is very little extra diffusion in 3D (some difference in the contact discontinuity is caused by the second versus third-order algorithm).

Original page by Ian Parrish, February 2004