

Orszag-Tang Vortex Test |
The problem was first studied by Orszag & Tang (J. Fluid Mech., 90, 129, 1998). Since then it has been extensively compared in tests of numerical MHD simulations. A few such examples include Zachary et al. (JSC, 15, 263, 1994), Ryu et al. (ApJ, 452, 785, 1995 and ApJ, 509, 244, 1998), Dai & Woodward (ApJ, 494, 317, 1998), Jiang & Wu (JCP, 150, 561, 1999), and Londrillo & Del Zanna (ApJ, 530, 508, 2000). The problem was also studied as a model for 2-D turbulence by Dahlburg & Picone, Phys. Fluid B, 1, 2153 (1989) and Picone & Dahlburg, Phys. Fluid B, 3, 29 (1991), using Fourier spectral methods.
We use a square domain, 0 ≤ x ≤ 1; 0 ≤ y ≤ 1. The boundary conditions are periodic everywhere. The density ρ is 25/(36π) and the pressure is 5/(12π) everywhere, and γ = 5/3. Note that this choice gives cs2 = γP/ρ = 1. The initial velocities are periodic with Vx = - Sin(2πy) and Vy = Sin(2πx). The magnetic field is initialized using a periodic vector potential defined at zone corners; Az = B0 (Cos(4πx)/(4π) + Cos(2πy)/(2π)), with B0 = 1/(4π)1/2. Face-centered magnetic fields are computed using B = ∇ ⊗ Az to guarantee ∇ ⋅ B = 0 initially. This gives Bx = -B0Sin(2πy) and By = B0Sin(4πx).
The Orszag-Tang vertex is a well-known model problem for testing the transition to supersonic 2D MHD turbulence. Thus, the problem tests how robust the code is at handling the formation of MHD shocks, and shock-shock interactions. The problem can also provide some quanititative estimates of how significant magnetic monopoles affect the numerical solutions, testing the ∇ ⋅ B = 0 condition. Finally, the problem is a very common test of numerical MHD codes in two dimensions, and has been used in many previous studies. As such, it provides a basis for consistent comparison of codes.
Results computed with Athena using the Roe solver and the third order algorithm on a 512x512 grid are shown below at time=0.1 (on the left), and time=1.0 (on the right). The images show the pressure on a linear color map between 0.01 and 0.7.
Click on the right image to download a .gif movie (28.8 MB).

|

|
The results for time=0.5 are shown below for a 64x64 grid (upper left), 128x128 grid (upper right), 256x256 grid (lower left), and 512x512 grid (lower right). The images show the density on a linear color map. (Note the image below contains all four results joined into one 1024x1024 image.)
They can be compared to Figure 6 of Dai & Woodward (1998), Figure 10 of Londrillo & Del Zanna (2000), and Figure 3 of Ryu et al. (1998) (taken at time=0.48).

|
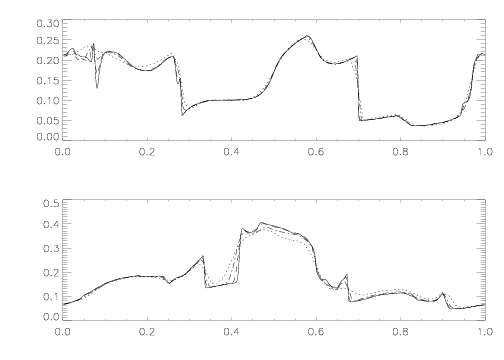
For more quantitative comparisons between schemes, we plot the value of the pressure in horizontal slices along y = 0.4277 and y = 0.3125 at time = 0.5. The horizontal axis is the x-axis and the vertical axis is the normalized pressure P. The results are shown for a 64x64 grid (dotted line), 128x128 grid (dot-dash line), 256x256 grid (dashed line), and 512x512 grid (solid line).
They can be compared to Figure 11 of Londrillo & Del Zanna (2000) and Figure 3 of Ryu et al. (1998) (taken at time=0.48) (see also Jiang & Wu 1999).
|