The Magnetic Field Loop Test |
A non-dynamic version of this test (non-dynamic in the sense that velocities are held fixed and only the induction equation is solved) was given by Toth, G. & Odstrcil, D., "Comparison of some flux corrected transport and total variation diminishing schemes for hydrodynamic and magnetohydrodynamic problems", JCP, 128, 82 (1996). Their test was based on an earlier version by DeVore (JCP, 92, 142, 1991).
The test described here is different in that the flow is fully dynamic, that is the entire MHD system (and not just the induction equation) is solved. This can produce oscillations that might not otherwise be present.
The test involves advecting a field loop (cylindrical current distribution) diagonally across the grid. Any arbitrary angle can be chosen. For the 2D results shown here, the problem domain is -1 ≤ x ≤ 1; -1/(2*cos(30)) ≤ y ≤ 1/(2*cos(30)), and the flow is inclined at 60 degrees to the y-axis. This geometry ensures the flow does not cross the grid along a diagonal, so the fluxes in x- and y-directions will be different.
The flow velocity is 1.0, so that Vx=sin(60) and Vy=cos(60). The density and pressure are both 1.0, and the gas constant is γ = 5/3. Periodic boundary conditions are used everywhere.
The magnetic field is initialized using an arbitrary vector potential defined at zone corners; we use Az = MAX([A ( R0 - r )],0). The amplitude A must be small so that the field is weak compared to the gas pressure. A stronger field would require a more careful choice of Az so that the loop is in magnetostatic equilibrium). We use A = 1.0e-3 and a radius for the loop R0 = 0.3. Face-centered magnetic fields are computed using B = ∇ ⊗ Az to guarantee ∇ ⋅ B = 0 initially. Note for the vector potential we have adopted, the second derivative (current density) is discontinuous. There is a line current at the center of the loop, and a surface return current. These currents are neither resolved nor smooth (see the images and movie below) -- if anything this makes the test harder. A different vector potential which gives smooth currents could be adopted for convergence tests.
This test demonstrates the importance of including the '∇ ⋅ B source terms' in the one-dimensional equations of motion. Most 1D MHD solvers make the assumption that ∂ Bx/∂ x = 0 and therefore ∂ Bx / ∂ t = 0 for the x-sweep, (and similarly for ∂ By / ∂ y during a y-sweep). However, this is manifestly not true in a multidimensional field geometry such as the loop initialized here. Whether these terms are required for any particular method depends on the details of the method. We find they are essential for both the PPM reconstruction and CTU unsplit integrator used in Athena. However, the 2nd-order VanLeer integrator (also implemented in athena3.0) does not require these terms. The terms are required whenever only a partial set of flux-differences instead of all the terms are added to the conserved quantities (for example, adding only the x-direction flux difference in 2D or 3D instead of the full set of x-, y-, and z-direction differences). See the Athena method papers for more details.
We have found that a particularly poweful test is to add a constant, uniform vertical velocity to the domain, and see whether Bz remains zero to round-off. This can only occur if the scheme preserves ∇ ⋅ B = 0 to round-off on the stencil actually used to update Bz. In this respect, this test defines what is the approriate stencil on which any scheme must preserve ∇ ⋅ B = 0.
The problem is essentially an advection test for the vector potential. Schemes which integrate the vector potential directly (rather than integrating the magnetic field components) should do very well on this test.
Results computed with Athena using a 256x148 grid are shown below. The Roe solver and 3rd order interpolation was used.
The contour plot on the left shows the initial magnetic field lines, using 20 contour levels. The image on the right is the field lines after the loop has been advected around the grid twice.
 |

|
Click on the image below to download a movie of the current density (6.2 MB) made with a linear color map between -0.04 and 0.08. The current is extremely sensitive to oscillations in the field components. We expect some evolution because the loop is not in exact magnetostatic equilibrium. Athena holds the shape of the loop very well.

A more quantitative diagnostic is the decay rate of the total magnetic energy. The plot below shows the evolution of the magnetic energy in a 128 x 64 grid computed using third order reconstruction. Time is shown in units of the grid crossing time.

Finally, as mentioned in the "What's important?" section, we have run this test in 2D with a uniform, non-zero value of Vz everywhere. This should not change the solution in any way. In particular, if Bz is initially zero, it must remain zero to round-off for all time. This is a non-trivial test, for in order for Bz to remain zero, the flux differences in the algorithm must cancel exactly. We find the CT algorithm we use, combined with unsplit integrators, does indeed keep Bz zero to round-off.
In 3D, we can repeat the 2D test described above; we get identical results (not shown here). More importantly, we have run the 2D test in 3D with a uniform, non-zero value of Vz everywhere. Again, this should not change the solution in any way. It is even more difficult to guarantee that the flux differences in the algorithm cancel exactly in 3D so that Bz remains zero. Again, we find the CT algorithm we use, combined with unsplit integrators, does indeed keep Bz zero to round-off.
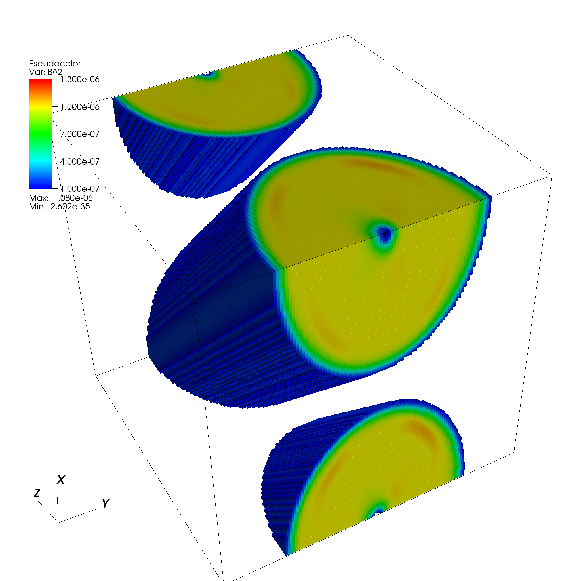
Another test in 3D is to use an inclined flux tube. We use a domain of size 1 X 1 X 1, with a 1283 grid. The field loop is initialized along the x-z diagonal of the grid. Periodic boundary conditions are used, with a flow velocity Vx = Vy = Vz = L/√ 3. The image below shows an isosurface of the magnetic energy density after one crossing time computed with 3rd-order HLLD. The geomtery of the loop is preserved extremely well. In addition, the component of the magnetic field projected along the axis of the cylinder in 3D should remain small: we find the volume-averaged magnetic energy associated with this component of the field is 3-4 orders of magnitude smaller than that associated with the "poloidal" field.