The Current Sheet Test

Reference:

Hawley, J.F., & Stone, J.M., Comp. Phys. Comm. 89, 127 (1995). As described in section 3.4, the test was used to improve the MOC-CT algorithm implemented in ZEUS.

Description:

The grid is square with -0.5 ≤ x ≤ 0.5 and -0.5 ≤ y ≤ 0.5. The density and pressure are uniform everywhere, with ρ = 1 and P = β/2 where β is an input parameter. For |x| > 0.25 we set B_y / (4π)^1/2 = 1, otherwise B_y / (4π)^1/2 = -1. The velocities are V_x = A sin (2πy) (where A is an amplitude) and V_y = 0. The "standard" test uses β = 0.1 and A = 0.1, although part of the point of this test is to see how small (large) a value of β (A) is required to break the code.

What's important about this test?

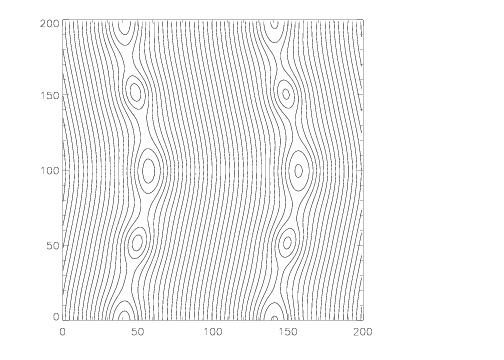
Although we do not know the analytic solution for this problem, we have found it to be an excellent test of the robustness of the algorithm. For ideal MHD, initially the solution should be nonlinear linearly polarized Alfven waves propagating along the field in the y-direction (which quickly generate magnetosonic waves since the magnetic pressure does not remain constant). However, because of the two current sheets in the problem (at x = ±0.25), reconnection inevitably occurs. Because β < 1, this reconnection drives strong over-pressurized regions that launch magnetosonic waves transverse to the field. Moreover, as reconnection changes the topology of the field lines, magnetic islands will form, grow, and merge. The point of the test is to make sure the algorithm can follow this evolution for as long as possible without crashing. Keeping ∇⋅B = 0 as the field toplogy undergoes complex changes could be important.

Results:

The plots below show the magnetic field lines at times of 2, 5, and 10 computed using a 100 x 100 grid using the Roe solver and the third order algorithm. We choose β = 0.1 and A = 0.1. The emergence and merging of magnetic islands is clearly visible.

T = 2

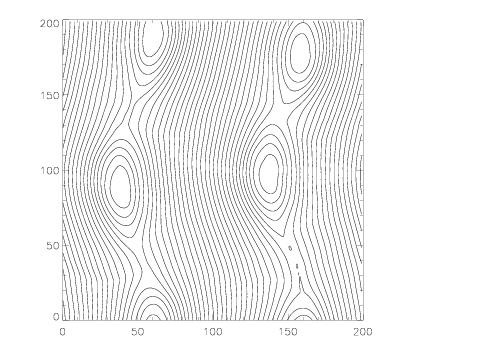T = 5

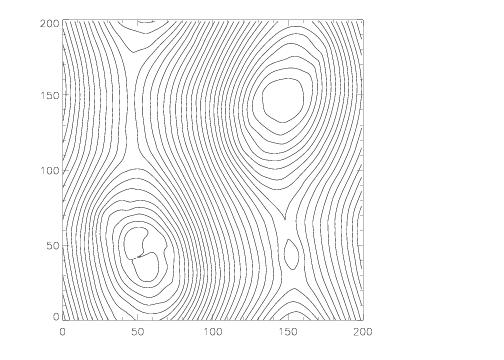T = 10

You can also downlad a movie of B_y (46 MB). The production of magnetosonic waves due to the dissipation of magnetic energy in the reconnection regions is clearly visible in the movie. Note that code that use an internal (rather than total) energy formulation (like ZEUS) do not produce such strong transverse waves.

The algorithms currently implemented in Athena cause the code to crash on this test at late times when β ≤ 5 x 10^-3, or when A ≥ 3.