  Try making a hyperbolic sheet as described here by William Thurston in his book Three-dimensional geometry and topology. " (a) Cut out a number of equilateral triangles from paper...and join them so that there are seven around each vertex. Alternatively, sew pieces of cloth together. " (d) These polyhedral models [described in (a)] have negative
curvature
concentrated at their verticies. You can make smoother models by
diffusing the curvature out along the edges: replace each side of the
equilateral triangles by an arc of circle such that the three sides of the
resulting curvilinear triangle are 2 If you choose not to draw your own template, here is a model curvilinear triangle that you may choose to print and cut out out. Glue, tape or sew 7 of these triangles together at each vertex to form a hyperbolic sheet. The first model is somewhat simpler even though it may not work as well
for the Curvature of the univere activities, you can still use the sheet
as a good example to show the class and the students will probably enjoy
helping to construct the sheet. You can save some time when constructing
this model by creating six equilateral triangles at once on the interior
of a regular hexagon and then inserting an extra (seventh) triangle. To
do this make a cut from one of the corners of the hexagon to the center of
the hexagon and tape or glue the to sides of this slit to the sides of
another equilateral triangle that is the same size as the six in the
hexagon. You should notice that the paper will no longer lie flat, this
is what causes the negative curvature. Go back to Curvature of the Universe Activity Go back to Curvature of the Universe Activity
II
|
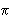 /7. (The radius of
the circle should be approximately 6.69 times the side of the
triangle.)"
/7. (The radius of
the circle should be approximately 6.69 times the side of the
triangle.)" 33
33