  Here is an explanation of how magnitudes and brightness are related which allows astronomers to work with the equation: d=10(m-M+5)/5 which is another way of writing B=L/(4 Consider two stars one of magnitude m1 and the other of magnitude m2. These stars also have brightnesses of b1 and b2 respectively. These brightnesses are related to the magnitudes: m2 - m1=2.5 * log(b1/b2). This is because for each difference in magnitude the ratio of brightness is different by a factor of 2.5. Now consider a star of apparent magnitude m (remember that is the magnitude as you measure it from earth) and apparent brightness b which is a distance d from Earth. Now imagine that same star at a distance D=10 parsecs from Earth. It now has magnitude M, which by definition is the absolute magnitude (the absolute magnitude is the magnitude you would observe the star to have if it were 10 parsecs away). It also now has apparent brightness B. Using the ratio equations from above, we see that : m-M=2.5*log(B/b). We also know from the inverse square law that: (B/b)=(d/10)2. Combining these two equations we see that: M=m-5log(d/10), where d is measured in parsecs. Solving this equation for d, we get: d=10(m-M+5)/5.  Back | Next |
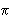 d2).
d2).