Sine and Cosine curves
Sine and Cosine curvesset x=0,3*pi,pi/30 set c=cos(x) set s=sin(x) limits x c box ctype red connect x c ctype blue connect x s ctype default set s=reverse(s) set rx=reverse(x) angle 90 shade 500 (x concat rx) (c concat s) angle 360 ylabel \Theta angle 0 xlabel x
10 terms of a square wave's Fourier series
# sum the Fourier series for a square wave, using $1 terms
set px=-pi,2*pi,pi/(10*$1 + 30)
set y=0
do i=1,2*$1-1,2{
set y=y+SIN($i*px)/$i
}
limits px -1.1 1.1
box
connect px y
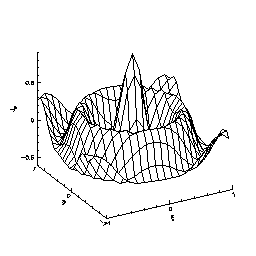Surface plot of a Bessel Function
image ( 21 , 21 ) -1 1 -1 1
set y=0,20
do x=0,20{
set r=sqrt((y- 10)**2 + ($x - 10)**2)
set image($x,y) = J0(r)
}
set x=abs($1) set t=x/3 set u=(t<1) ? t**2 : 1/(t+1e-9)
set v=u/3
set $0=(t<1) ? 1 + \
u*(-2.2499997+u*( 1.2656208+u*(-0.3163866+ \
u*( 0.0444479+u*(-0.0039444+u*0.00021))))) : \
(0.79788456+u*(-0.00000077+u*(-0.0055274 +u*(-0.00009512+ \
u*( 0.00137237+u*(-0.00072805+u*0.00014476))))))* \
cos(x-0.78539816+u*(-0.04166397+u*(-0.00003954+u*(0.00262573+ \
u*(-0.00054125+u*(-0.00029333+u*0.00013558))))))*sqrt(v)
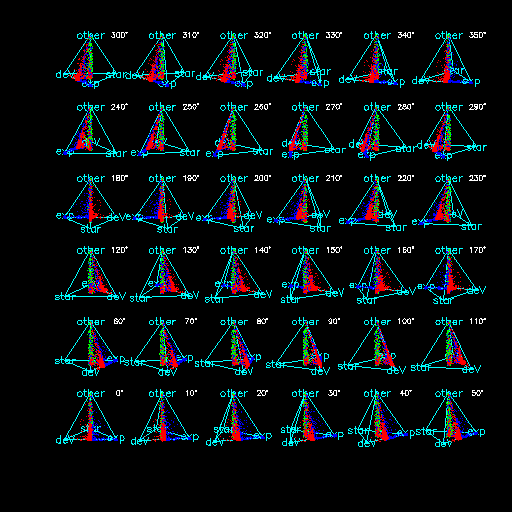
The macros to plot this are quite long... Here's the top level macro:
LtetraType3dAll 01 # call LtetraType for all angles in 0..360 (10)
define a local
do a=0,359,10 {
set_window -6 -6
if($?1) {
LtetraType 15 $a $1
} else {
LtetraType 15 $a
}
relocate $($fx1 + 0.9*($fx2-$fx1)) $($fy1 + 0.9*($fy2-$fy1))
putl 5 \-2$a^\circ
}
window 1 1 1 1
It calls LtetraType:
LtetraType 23 # draw a tetrahedral diagram colour coded by type
set _l local
if($?3) {
set _l = $3 # before we make Lstar etc. local
} else {
define 3 _l set _l=1+0*Lexp
}
tetraBox $1 $2 deV exp star
expand $($expand/2)
ctype green tetraPoi $1 $2 type=='star'&&_l
ctype blue tetraPoi $1 $2 type=='exp'&&_l
ctype red tetraPoi $1 $2 type=='deV'&&_l
ctype 0
expand $($expand*2)
which calls 2 macros:
tetraBox 5 # Draw a box for a triangle plot
# Usage: tetraBox theta phi L1 L2 L3
lim -0.7 0.7 -0.7 0.7
ctype cyan
set x local set y local set z local
set x=<-0.5 0.5 0 0>
set y=<$(-1/3*sqrt(3/4)) $(-1/3*sqrt(3/4)) $(2/3*sqrt(0.75)) 0>
set z=<$(-1/3*sqrt(3/4)) $(-1/3*sqrt(3/4)) $(-1/3*sqrt(3/4))\
$(2/3*sqrt(3/4))>
set x_p local set y_p local set z_p local
rotate x y z x_p y_p z_p $1 $2
set s local
define ptype local define ptype |
set s=<" $!3 " " $!4 " " $!5 " "other"> ptype s
poi x_p z_p
ptype $ptype
set s=0,3 set y=y_p if(s < 3) set s=0,2
sort { y s }
RELOCATE $(x_p[3]) $(z_p[3])
define i local
foreach i ($(s[1]) $(s[0]) $(s[2]) 3 $(s[0])) {
DRAW $(x_p[$i]) $(z_p[$i])
}
lt 1
RELOCATE $(x_p[s[1]]) $(z_p[s[1]])
DRAW $(x_p[s[2]]) $(z_p[s[2]])
lt 0 ctype 0
#
tetraPoi 23 # Draw points for which $3 is true into a tetrahedron; the
# viewpoint is (theta, phi) = ($1, $2)
define v local
set _l local
if($?3) {
set _l = $3 # before we make Lstar etc. local
} else {
define 3 _l set _l=1+0*Lexp
}
set x local set y local set z local
set tot local
set tot=Lexp+LdeV+Lstar
set x=(Lexp-LdeV)/(2*tot)
set y=(Lstar/tot - 1/3)*sqrt(3/4)
set z=Lexp > LdeV ? (Lexp > Lstar ? Lexp : Lstar) : \
(LdeV > Lstar ? LdeV : Lstar)
set z = 1 - z
set x=x*(1-z) set y=y*(1-z)
set z=sqrt(3/4)*(z - 1/3)
set random 0
foreach v {x y z} {
set $v = $v + 5e-2*(random(dimen($v))-0.5)
}
set x_p local set z_p local
project x y z x_p z_p $1 $2
if('$ptype' != '1 1') {
ptype 4 0
}
poi x_p z_p if($3)
if('$ptype' != '1 1') {
ptype 4 1
}
#
And that's almost it; rotate and project are in the standard utils package
Dithered Image of the Galaxy M51image m51_g.fts define min 3000 define max 60000 define gamma 2 set ii = image[*,*] set ii=(ii < $min ? 0 : ii > $max ? 1 : (ii-$min)/($max - $min) set image[*,*] = (1 + $gamma)*ii/(1 + $gamma*ii) dither x y 0 1 3 range 400 400 limits x y ptype 1 1 points x y