Accretion flows are ubiquitous in astrophysics: they occur around protostars, accreting compact objects in binary systems, and supermassive black holes at the cores of galaxies. Much of my work has concerned studies of the local hydrodynamic and MHD processes that can lead to outward angular momentum transport in accretion disks. As computers become more powerful, previous studies of local patches of an accretion flow are being expanded into global studies that encompass the entire disk.
The work shown here has been done in collaboration with Steve Balbus (UVa), Mitch Begelman (CU), Charles Gammie (UIUC), John Hawley (UVa) and Jim Pringle (IoA, Cambridge)
Vertical convection can occur in an accretion disk if a sufficiently steep entropy gradient is established via cooling of the surface layers by optically thin radiation. To study whether hydrodynamical turbulence generated by strong convection can transport angular momentum in disks, 3D direct numerical simulations of nonlinear convective in a local patch of a shearing disk were performed.
The image shows the magnitude of vertical velocities on three slice planes through the computational volume. Red regions are updrafts, blue regions are downdrafts. The convective eddies are clearly stretched into long, thin sheets in the azimuthal direction via shear.
Surprisingly, the time-averaged Reynolds stress for driven convective turbulence in a Keplerian disk is both small and negative, indicating angular momentum is transported inwards, if at all.More detail can be found in the following papers:
``Angular Momentum Transport in Accretion Disks by Convection", by J.M. Stone & S.A. Balbus, The Astrophysical Journal, 464, 364 (1996).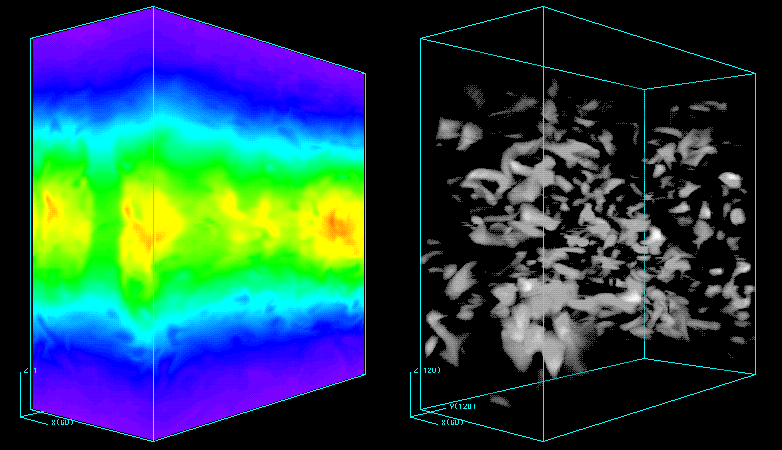
Angular momentum transport in accretion flows is mediated
by MHD turbulence driven by the Balbus-Hawley (or magnetorotational)
instability (MRI). To study the nonlinear regime of the MRI in vertically
stratified disks, 3D MHD simulations were performed. As in
unstratified flows, the MRI saturates as anisotropic MHD turbulence.The image above shows the density (as colors) on two surfaces of the computational volume, and a volumetric rendering of the magnetic pressure throughout the computational domain, after 20 orbits of evolution of an initially weak vertical seed field. The image below again shows the density, as well as magnetic field vectors along a horizontal slice just below the disk midplane. Click on either image to download a full-sized version.
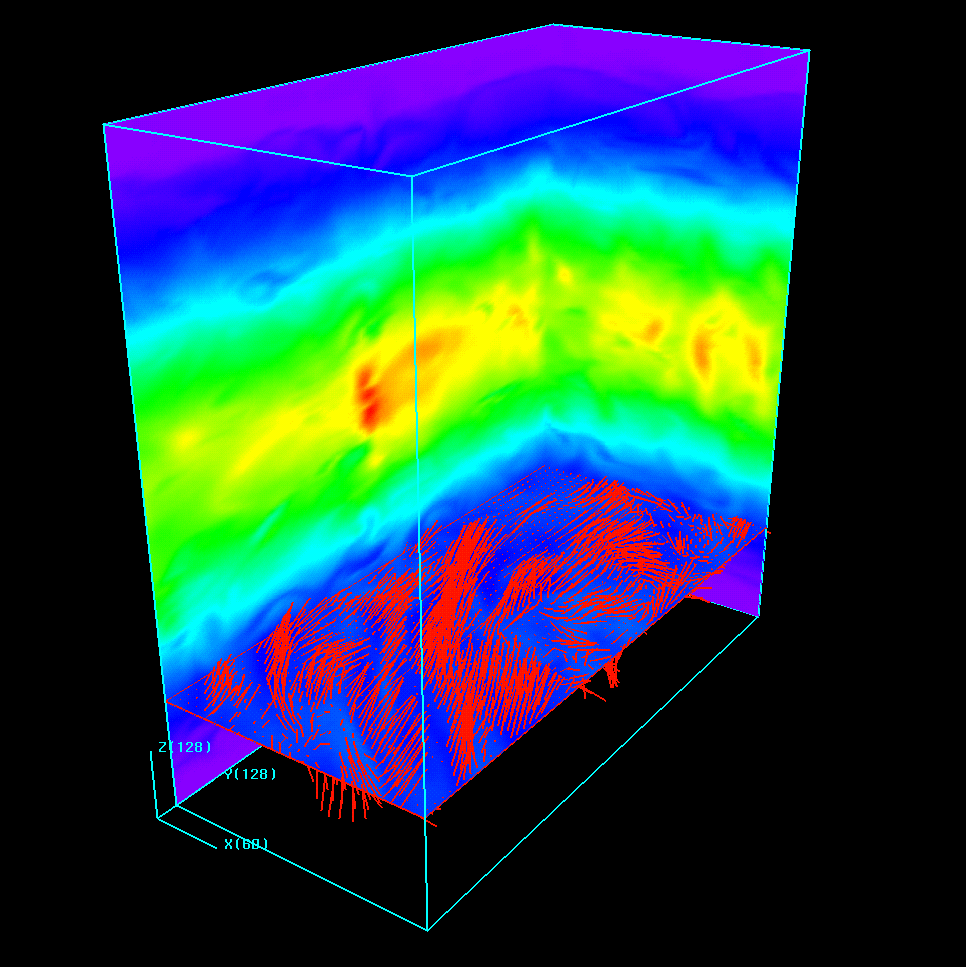Stratification seems to make little difference on the properties of the
turbulence or the angular momentum transport rate. Buoyant rise of
flux is seen, leading to stronger magnetic fields above and below
the disk than in the midplane. But since these simulations only span
two scale heights above and below the midplane, the contrast is not enough
to produce a magnetically dominated disk corona.
Graduate student Kristen Miller has used new numerical methods to follow the evolution of the MRI in vertically stratified disks over five scale heights above and below the midplane. In this case, a magnetically dominated corona (with magnetic pressure much bigger than gas pressure) is produced by the disk dynamo.
More detail can be found in the following papers:
``Three Dimensional Magnetohydrodynamical Simulations of Vertically Stratified Accretion Disks", by J.M. Stone, J.F. Hawley, S.A. Balbus, & C.F. Gammie, The Astrophysical Journal, 463, 656 (1996).
Accretion flows that cannot cool via emission of radiation become vertically thick and nearly spherical. Thus, they are intrinsically multidimensional. To study the structure and evolution of non-radiative accretion flows, 2D (axisymmetric) hydrodynamical simulations were performed using a non-uniform grid that spanned more than two decades in radius.
The image below shows a snapshot of the density (left panel), entropy (middle panel), and angular momentum compared to Keplerian (right panel) in the inner 10% of the flow at late times. You can also download a movie of the density in either MPEG format (1.3Mb) or animate gif format (13Mb).
The most striking property of the flow is the large fluctuations produced by strong convection. Convective eddies transport a lot of mass both inwards and outwards, but the net mass accretion rate is very small and set by the properties of the flow near the inner boundary. A vanishingly small accretion rate may help to explain the deficit of high energy emission observed from accreting compact sources.
More detail can be found in the following paper:
``Hydrodynamic Non-Radiative Accretion Flows in Two-Dimensions", by J.M. Stone, J.E. Pringle, & M.C. Begelman, Monthly Notices of the Royal Astronomical Society, 310, 1002 (1999)
While understanding the properties of hydrodynamical accretion flows is important, it is generally agreed that angular momentum transport is in fact mediated by magnetic stresses. Thus, repeating the global simulations of non-radiative accretion flows described above with MHD calculations is vital.
The image below shows a snapshot of the density (left panel), entropy (left middle panel), toroidal magnetic pressure (right middle panel), and Maxwell stress normalized to the magnetic pressre (right panel) in the inner 10% of the flow at late times. You can also download a high time-resolution movie of the density in either MPEG format (2.1Mb) or animate gif format (14Mb). The same grid and initial conditions are used for this MHD model as were used for the hydrodynamical simulations, allowing direct comparison of the results.
Once again, we find the instantaneous structure of the flow is complex and highly time-variable, mostly as the result of turbulence driven by the magnetorotational instability. The two-dimensional structure of the time-averaged flow is considerably different than the hydrodynamical case, although many other properties, such as the net mass accretion rate, are similar (once again, it is very small and set by the dynamics at the inner edge of the disk).
More detail can be found in the following paper:
``Magnetohydrodynamic Non-Radiative Accretion Flows in Two-Dimensions", by J.M. Stone, & J.E. Pringle, submitted to Monthly Notices of the Royal Astronomical Society